On March 11, Bruno (@bsudret), Xujia (@xujia) and Nora (@nluethen) took part in the virtual Workshop on “Stochastic simulators” organized by the research network GdR MASCOT-NUM.
GdR MASCOT-NUM (Méthodes d’Analyse Stochastique pour les COdes et Traitements Numériques, see also @biooss 's UQWorld post) is a French association for research on stochastic methods for the analysis of computational models. Among other activities, it coordinates research efforts and organizes conferences and workshops in the broad field of design and analysis of stochastic computer experiments.
We at RSUQ are working on stochastic simulators since 2017, when the SNF project SAMOS (Surrogate modelling for stochastic simulators) started. Two PhD students (Xujia and Nora) and one PostDoc (@c.lataniotis) are working on different aspects on how to construct surrogate models for stochastic simulators, utilizing our group’s expertise on surrogate modelling for deterministic simulators. In the engineering community, work on stochastic simulators is still scarce. Hence, it was extra exciting for us to take part in an event specifically devoted to this topic!
The workshop on stochastic simulators gave eight researchers the opportunity to present their recent work on surrogate modelling, sensitivity analysis, inverse problems, and optimization of stochastic simulators. We are happy and proud to have contributed three of those eight talks, and sincerely thank the organizers of this workshop, Anthony Nouy, Clémentine Prieur, and in particular Julien Bect, for making this exchange possible. In the following, we give a short summary of the topics and ideas that were discussed during this day. Abstracts and slides for the presentations can be found on the workshop’s website.
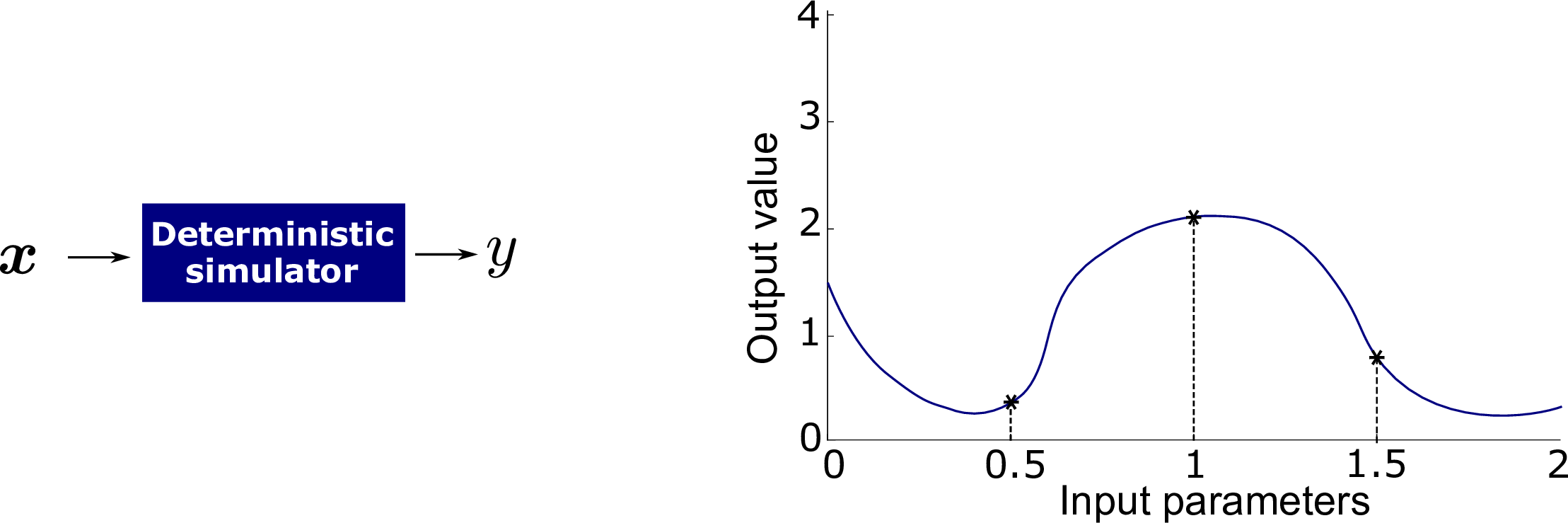
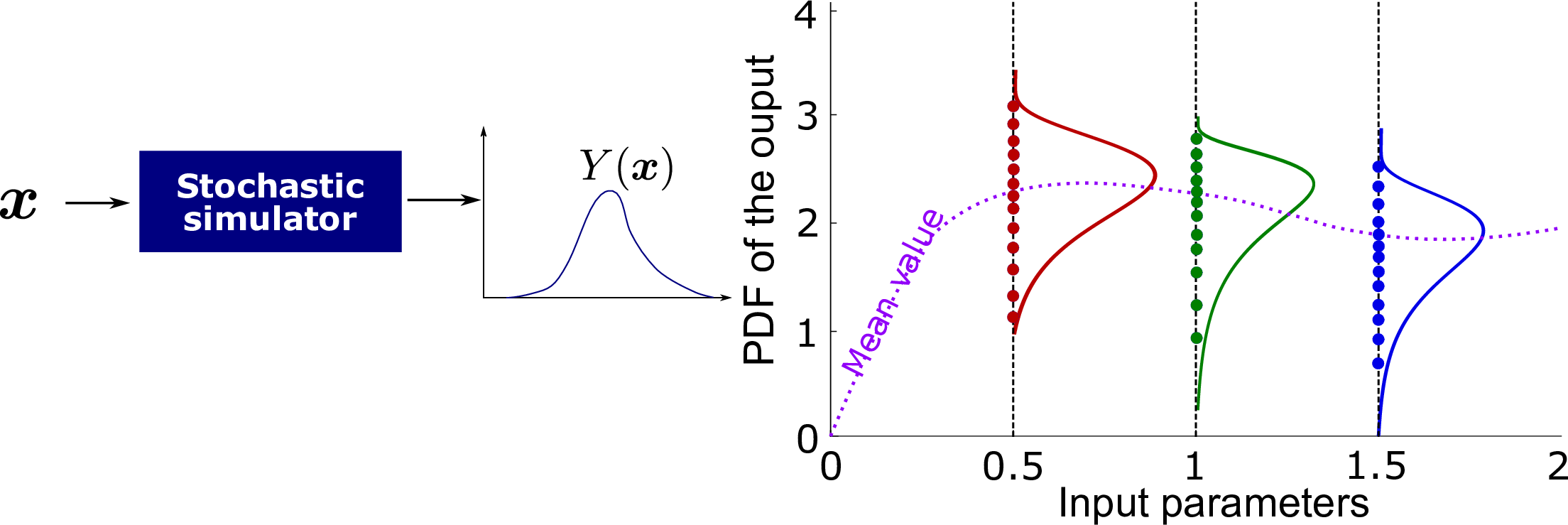
The workshop started off with a presentation by Bruno, who first addressed the basic question - what is a stochastic simulator, and why are we interested in it? Basically, a stochastic simulator is a computational model for which not all of its uncertain inputs are explicitly quantified. This might be because some of the variables affecting the model are too high-dimensional to be modelled probabilistically (e.g., wind fields or earthquakes), or because the model contains intrinsic randomness (e.g., epidemiological models). In contrast to a deterministic computer model, which for a fixed input vector always gives the same response, a stochastic simulator returns a distribution of response values even if the input vector is held fixed (see illustration below). We refer the interested reader to Xujia’s UQWorld article “Stochastic simulators: an overview” for a more detailed introduction to stochastic simulators.
After giving a structured overview of the literature on the topic of surrogate modelling for stochastic simulators, Bruno presented in detail Xujia’s and his joint research on surrogating stochastic simulators using generalized lambda models. The idea of this approach, called GLaM, is to model the response probability density function (PDF) of the stochastic simulator with the flexible lambda model, which is able to approximate many parametric distribution families as long as they are unimodal. The four parameters of the lambda model are surrogated by a polynomial chaos expansion (PCE) over the input domain. Bruno explained the difference between replication-based and replication-free methods and demonstrated the impressive efficiency of the GLaM method, even when compared to state-of-the-art conditional density estimation and applied to realistic computer models.
Next, Xujia presented his work on stochastic polynomial chaos expansions for emulating stochastic simulators. In this model, the classical PCE is extended to approximating the response distribution of stochastic simulators. To this end, both a latent and an additional noise variable, on top of the well-defined input parameters are introduced to represent the randomness in the model output. This surrogate is able to represent multimodal distributions. Maximum likelihood estimation and cross-validation are combined to adaptively build such a surrogate without the need for replications. The method shows good performance compared to the generalized lambda model and the state-of-the-art kernel estimator.
In the second session, Henri Mermoz Kouye gave a talk on sensitivity analysis for stochastic simulators with a focus on the SARS-CoV-2 model. The simulated stochastic process can be represented by Sellke construction or Kurtz representation, which allows for measuring the influence of both the model inputs and the intrinsic randomness on the global variability of the model output.
Then, Aurélien Garivier presented his research on optimizing noisy black-box functions. The ultimate goal is to find a sampling strategy which with high probability and as few function evaluations as possible allows to find a solution whose function value is at most epsilon away from the optimal solution (“probably approximately correct” setting) for discrete functions such as functions on graphs.
After the lunch break, the workshop continued with a presentation by Nora on surrogate modelling using a random field view of stochastic simulators, with the input parameter space acting as the index set of the family of random variables. Under a few regularity assumptions on the random field, it allows a representation by Karhunen-Loève expansion (KLE). In her approach, the costly computation of KLE eigenfunctions and -values is simplified by using PCE approximations of the stochastic simulator trajectories, which are known only through a finite number of model evaluations. The distribution of KLE random variables in the reduced space are rigorously inferred using parametric inference of marginals and vine copulas.
Athénaïs Gautier presented her work on logistic Gaussian processes as a surrogate modeling method for representing the response distribution of a stochastic simulator. More precisely, the conditional distribution is modeled as the logistic transform of a Gaussian process, which is discretized using a finite-rank expansion. The construction of this surrogate consists in estimating the posterior distribution of the random variables (with standard normal distribution as prior) in the expansion of the Gaussian process, which is carried out by MCMC sampling. This method combined with approximate Bayesian computation can be used to solve stochastic inverse problems.
In the fourth and last session of the day, Mickaël Binois talked about tackling multi-objective optimization for stochastic simulators. The objective functions are the mean functions of the random outputs. The heteroscedastic Gaussian process is used as a local surrogate to deal with big data. For each iteration of the proposed algorithm, part of the computational budget is allocated to performing replications for non-dominated points. In parallel, the rest of the budget is distributed according to a portfolio allocation scheme based on the expected hypervolume improvement.
Finally, Bruno Barracosa presented his work also on multi-objective optimization in the context of stochastic simulators. In the developed method, the outputs are assumed to be Gaussian and homoscedastic, and Pareto Active Learning (PAL) is used to guide the model evaluation.