Further plot possibilities for results of Bayesian inversion (Suggestions and code example)

[olaf.klein]

Dear UQLab-Team,

thanks for your efforts to created the UQLab Modules 1.4.0,

I would like to suggest to add further plot output facilities for results of Bayesian inversion performed by the evaluation of uq_createAnalysis, and I provide a code example as a kind of proof of concept.

I suggest to help users to generated plots

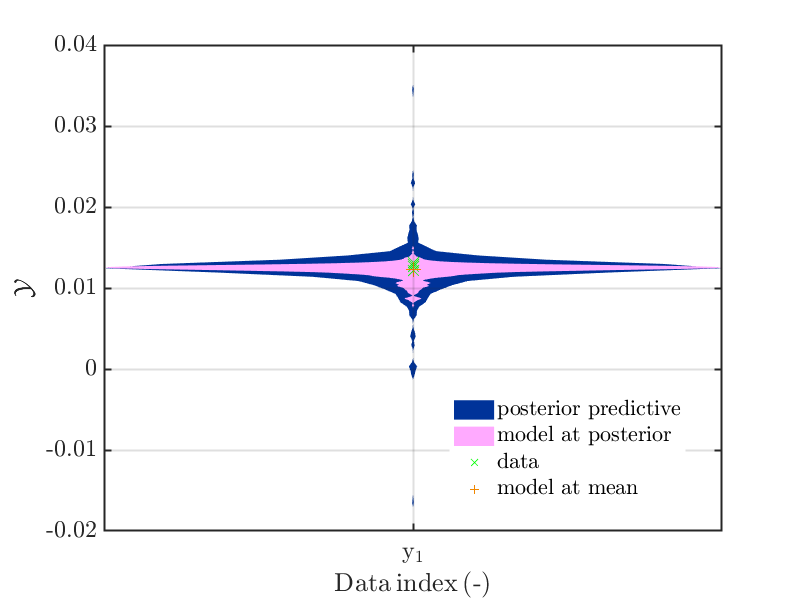
• showing the density of the model evaluation the samples computed to represent the posteriori density, and plots comparing this density with the posteriori density;
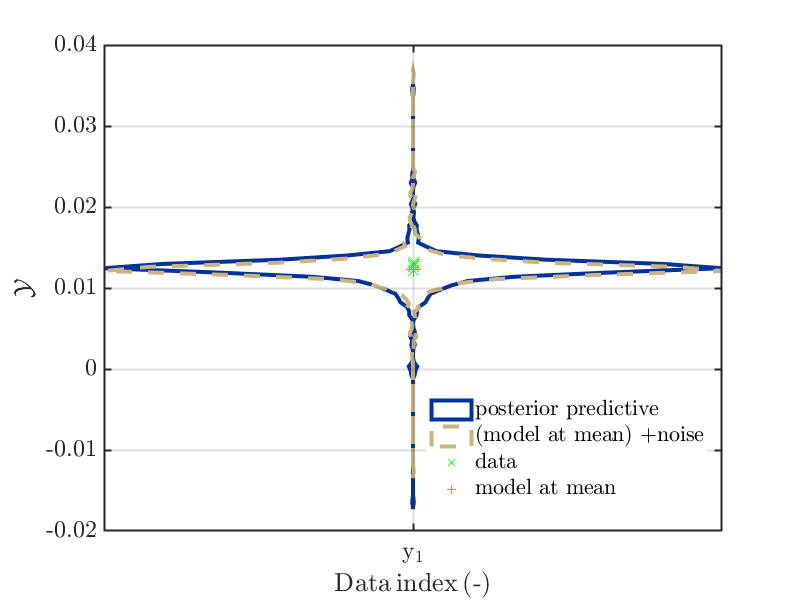
• showing the density resulting fron adding noise to the value of the model at the (first) considered point estimate and plots comparing ths density with the posteriori density;
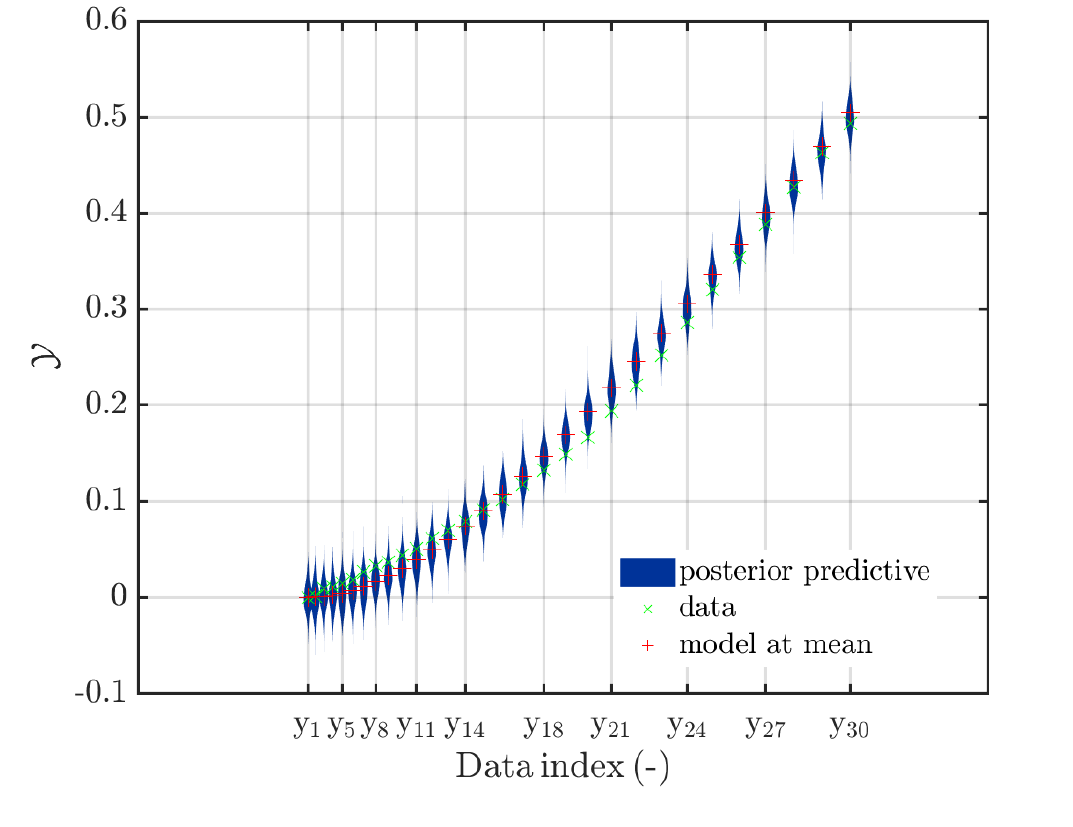
• of some subrange of the considered indices.

As a proof of concept that could also be of use for other UQLab users, I present
a modified version of the function plotSeriesPred.m from the UQLab File uq_display_uq_inversion.m in the file mod_UQLab_plotSeriesPred_2021.m (11.3 KB) such that appropriate calls to this function generate the suggested kinds of plots.

(This post is an update of the post in .Bayesian inference in UQLab: suggestions for improving the plot functions and the corresponding UQLab User Manual - #3 by olaf.klein to UQLab Modules 1.4.0 with some improvements, since the code in the old post relied on some update for UQLab 1.3. that was used only by very few people.)

New function in file mod_UQLab_plotSeriesPred_2021.m

I modified the function plotSeriesPred.m to get access to further informations produced during the Bayesian inversion performed by the evaluation of uq_createAnalysis and created the function mod_UQLab_plotSeriesPred_2021.m (11.3 KB)

One point is to consider on one hand the variation of the posterior predictive samples, i.e. the sum of the model output at the samples and appropriate noise and on the other hand the variation of the model outputs at these samples only.

Moreover, one may need information to decided how to perform further computations using the results of the Bayesian inversion. Here one has to decide, if one should perform a forward UQ computation or if one can expect to derive similar results by performing a reduced forward UQ computation, i.e. by evaluating the model only at a point estimate for the parameters, like the mean of posterior density or the MAP value, and adding afterwards some noise values to the resulting model value.

To decide this, I think that one should investigate to the results of the Bayesian inversion from an other point of view: The resulting posterior predictive density is the density one one would get from the output of a (full) forward UQ computation for the considered model using the the density represented by the derived samples for the parameter values.
Moreover, by adding the discrepancy samples used for the computation of the posteriori prediction samples to the model output either for the mean of the posterior density or MAP point estimate, one can compute the results corresponding to a reduced forward UQ computation.

If these densities are quite different, one can expect that also in other situations the results of a reduced forward UQ computation will not generated good approximations for the results for a (full) forward UQ computation. But, if the results are similar then I think that there is some chance/risk that the results of the reduced forward Uq computation allow to approximate the results for the full forward UQ computation. This can be good news, if one is only interested to compute this approximation. But, this can also be bad news, if the considered problem was planed to promote dealing with UQ considerations.

I think that this function may also be helpful for other users of UQLab.

The original version of this function was developed for UQLab 1.3.0 combined with some update file provided by Paul-Remo (thanks again), and has now be adapted to UQLab 1.4.0 and some further improvements has been performed.

The modified function in `mod_UQLab_plotSeriesPred_2021.m’ has the following features;

1. The output for all plot types can be restricted to show only data points within a given index range.

2. The density of the model evaluations at the samples of the posterior ensity, i.e. the contents of myBayesianAnalysis.Results.PostProc.PostPredSample.Post,
   can be ploted, see the examples with 'model' as plot type parameter, i.e. as third parameter.

3. The normal posterior predictive density plot can be combined with the density discussed in the last point. This allows to decide if the variation shown for a data point contain mainly the variation due to the noise or if the value of the model also shows significant variations due to variation of the parameter values. This can be achieved by using 'post&Mod' as plot type parameter.

4. To check if the reduced forward UQ computations can be expected to generate relevant outputs, one can evaluate the model at the point estimate and add afterwards noise to the resulting value. This noise is just the difference between the values in myBayesianAnalysis.Results.PostProc.PostPredSample.PostPred and myBayesianAnalysis.Results.PostProc.PostPredSample.Post. This can be achieved by using 'Model(PE)+noise' as plot type parameter.

5. One can combine the posteriori predictive density and the density discussed in the point before into one plot by
   using 'post&Model(PE)+noise' or 'post&Model(PE)+noise:edges' as plot type parameter to create a combination of the normal violin plots or a combination of two plots showing
   the boundaries of the domain shown in violin plots only, using a dashed linef or the 2nd ploted boundary.

6. Using 'prior' or 'post' as plot type parameter one can generate post of the prior density (if samples are given) or of the posteriori density. Hence, one can generate a plot of the posterior density alone without needing to call ‘‘uq_postProcessInversion’’ to remove the posteriori density points, and to change also the considered samples.
   The combination can be ploted using 'prior&Post' (with an ampersand) as plot type parameter.

7. If more the one value for the point estimator is given, the marker for model value at the first point estimate is a cross, as in the normal UQLab version,
   the marker for 2nd, the 3rd, … point estimate is a triangle, such that the position of the model value at the first point estimate and at the second estimate can be seen even if the these values are almost identical.

Example: Hydrological model calibration

To start to consider the examples for Hydrological model calibration at https://www.uqlab.com/inversion-hydrological-model further, one can use the following commands:

uq_Example_Inversion_03_Hydro 
% Using the UQLab Modules 1.4.0 feature to deal with Mean and MAP point estimate at the same time
uq_postProcessInversion(myBayesianAnalysis, 'burnIn', 0.75,'pointEstimate',{'Mean','MAP'})

uq_display(myBayesianAnalysis)

The posterior predictive density plot will look like

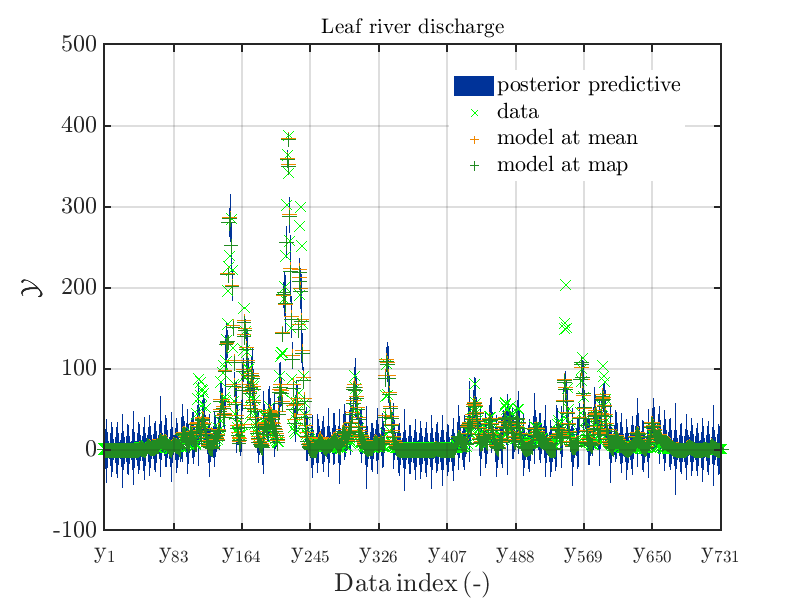
One can investigate the approximation of the Leaf river discharge either by using the zoom in feature in the matlab graphics window or by the commands

% Copying data int local variables to be used as input for
% mod_UQLab_plotSeriesPred_2021 in the following
myData = myBayesianAnalysis.Data
mySamples.PostPred= myBayesianAnalysis.Results.PostProc.PostPredSample.PostPred
mySamples.Post= myBayesianAnalysis.Results.PostProc.PostPredSample.Post

myPointEstimate=myBayesianAnalysis.Results.PostProc.PointEstimate.ForwardRun

% frist set of plots: Normal plots of posterior density, restricted to some index ranges,:
mod_UQLab_plotSeriesPred_2021(mySamples,myData,'post',myPointEstimate,1,100)
title('Leaf river discharge');

mod_UQLab_plotSeriesPred_2021(mySamples,myData,'post',myPointEstimate,100,200)
title('Leaf river discharge');

mod_UQLab_plotSeriesPred_2021(mySamples,myData,'post',myPointEstimate,200,300)
title('Leaf river discharge');

mod_UQLab_plotSeriesPred_2021(mySamples,myData,'post',myPointEstimate,300,400)
title('Leaf river discharge');

mod_UQLab_plotSeriesPred_2021(mySamples,myData,'post',myPointEstimate,400,500)
title('Leaf river discharge');
    
mod_UQLab_plotSeriesPred_2021(mySamples,myData,'post',myPointEstimate,500,600)
title('Leaf river discharge');

mod_UQLab_plotSeriesPred_2021(mySamples,myData,'post',myPointEstimate,600,700)
title('Leaf river discharge');
 
mod_UQLab_plotSeriesPred_2021(mySamples,myData,'post',myPointEstimate,700,750)
title('Leaf river discharge');

These commands generate get a series of 7 plots showing the evolution in more detail:

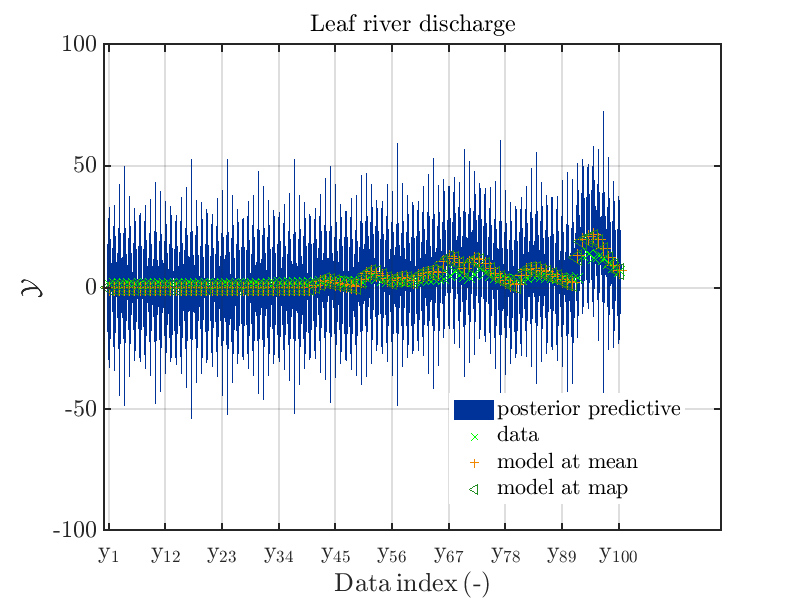
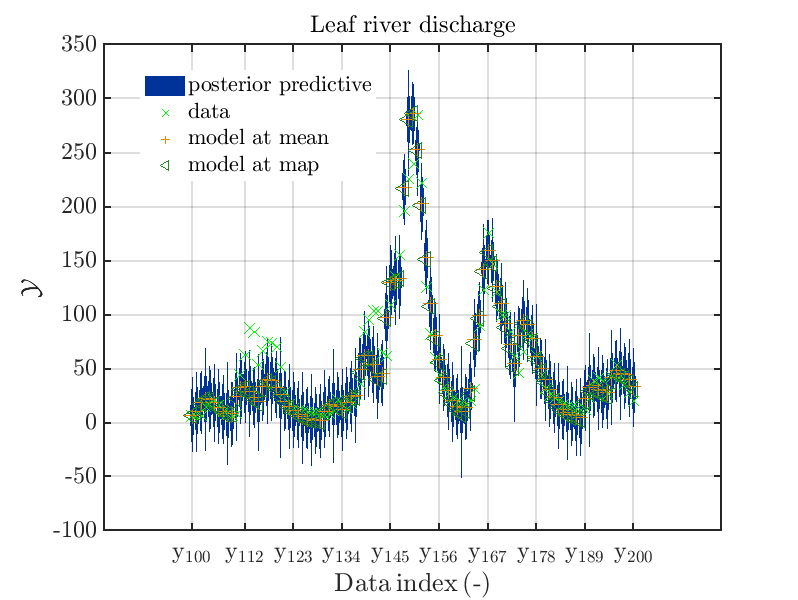
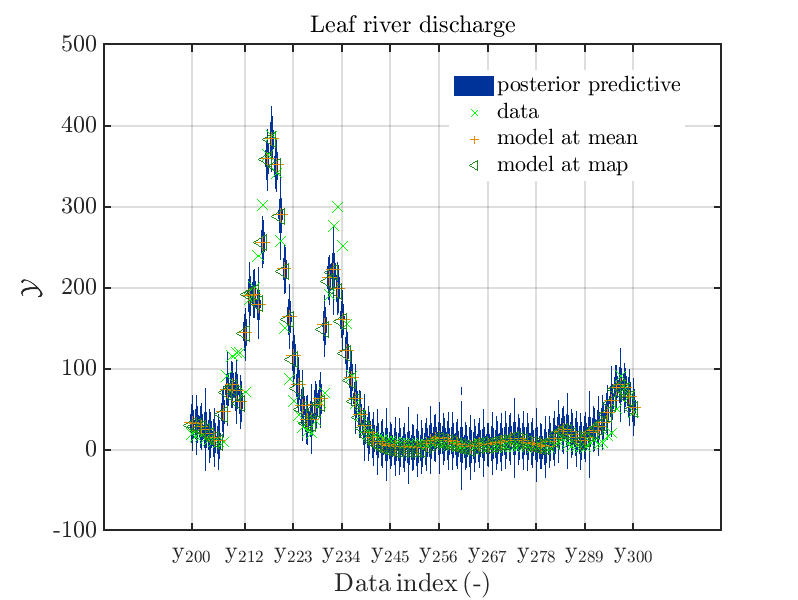
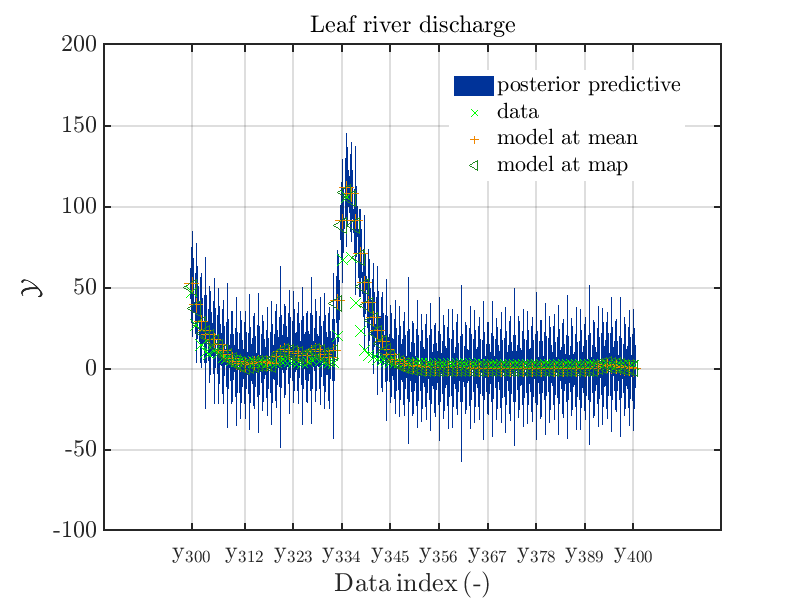
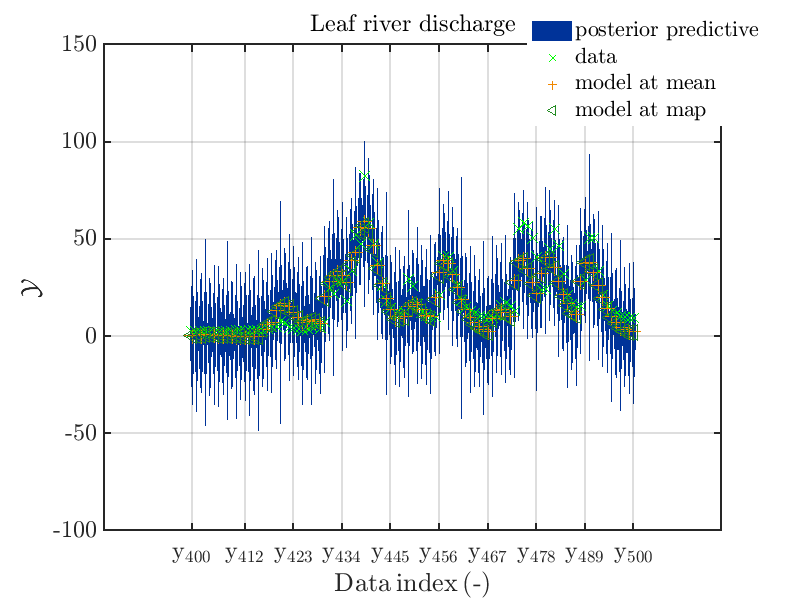
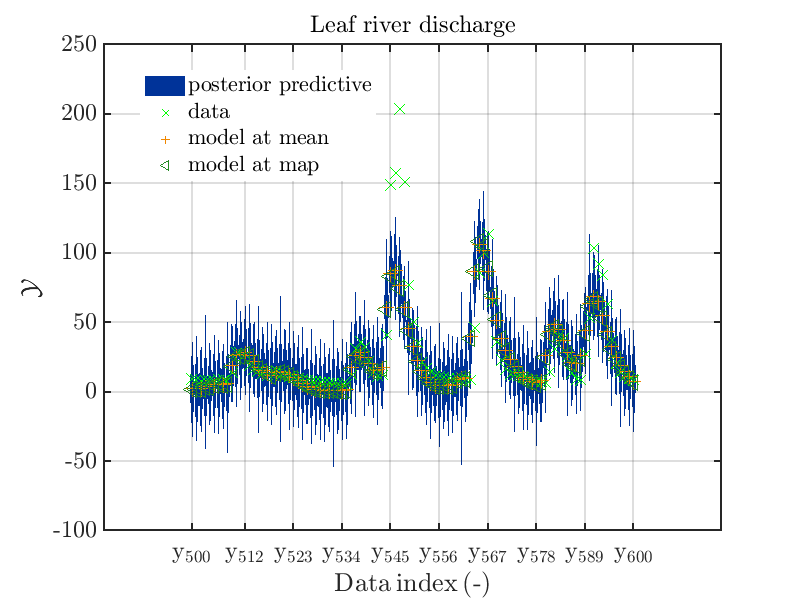
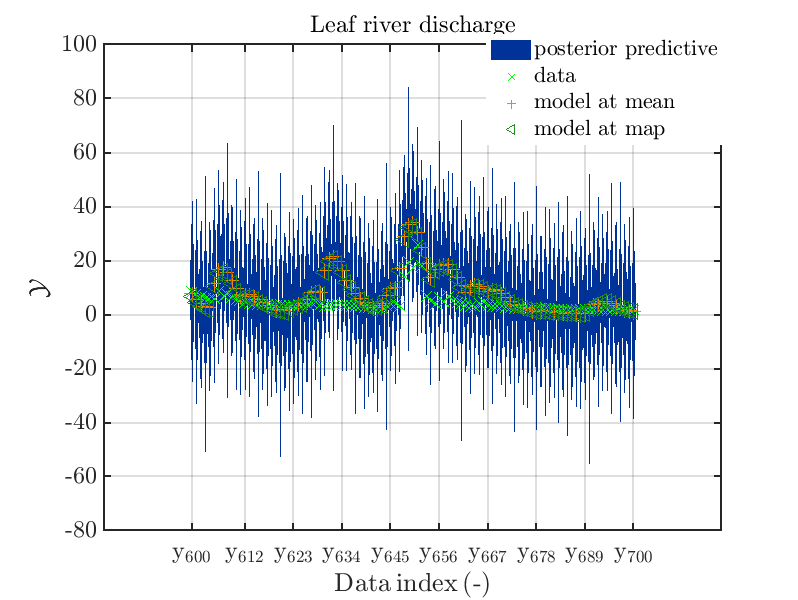
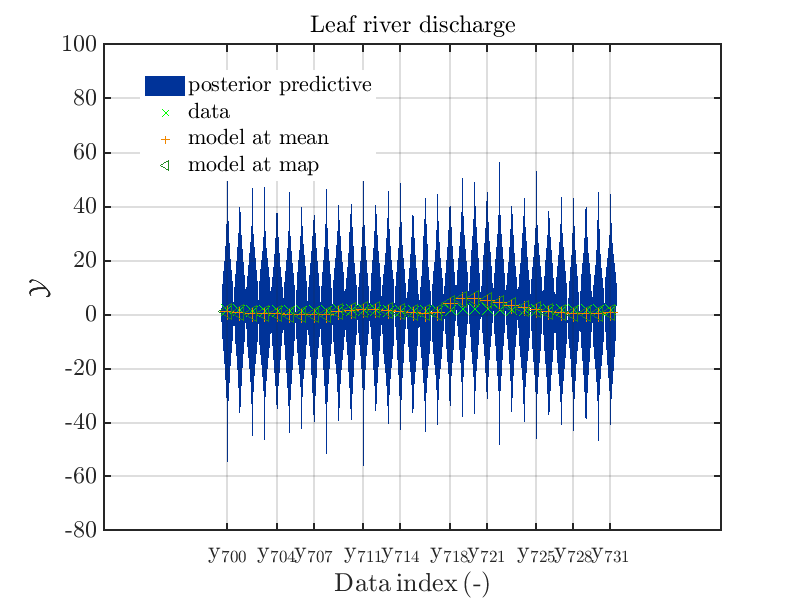
Considering fo some sub data ranges the density of the outputs of the model at the samples for the parameters for the HYMOD watershed model one can get corresponding plots by the commands

mod_UQLab_plotSeriesPred_2021(mySamples,myData,'model',myPointEstimate,25,50)
title('Leaf river discharge');

mod_UQLab_plotSeriesPred_2021(mySamples,myData,'model',myPointEstimate,125,150)
title('Leaf river discharge');
      
mod_UQLab_plotSeriesPred_2021(mySamples,myData,'model',myPointEstimate,200,250)
title('Leaf river discharge');
   
mod_UQLab_plotSeriesPred_2021(mySamples,myData,'model',myPointEstimate,600,650)
title('Leaf river discharge');

Comparing the resulting plots




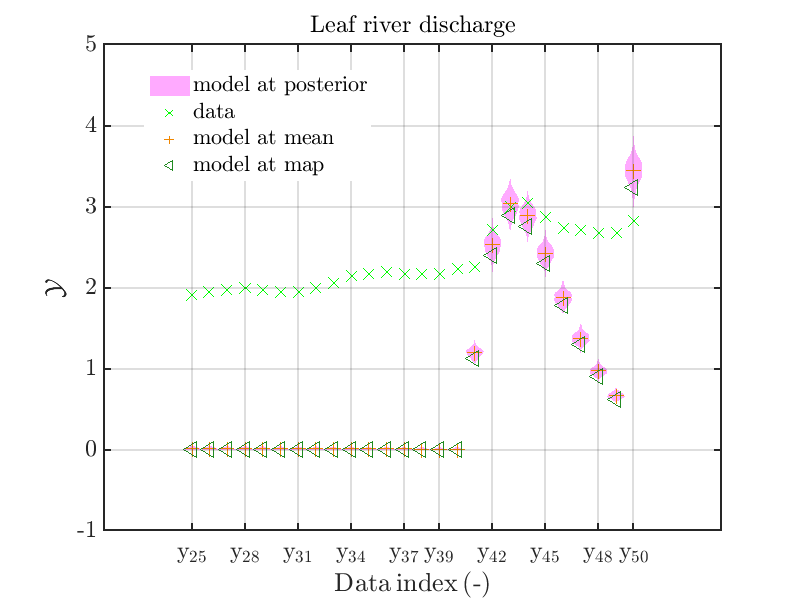
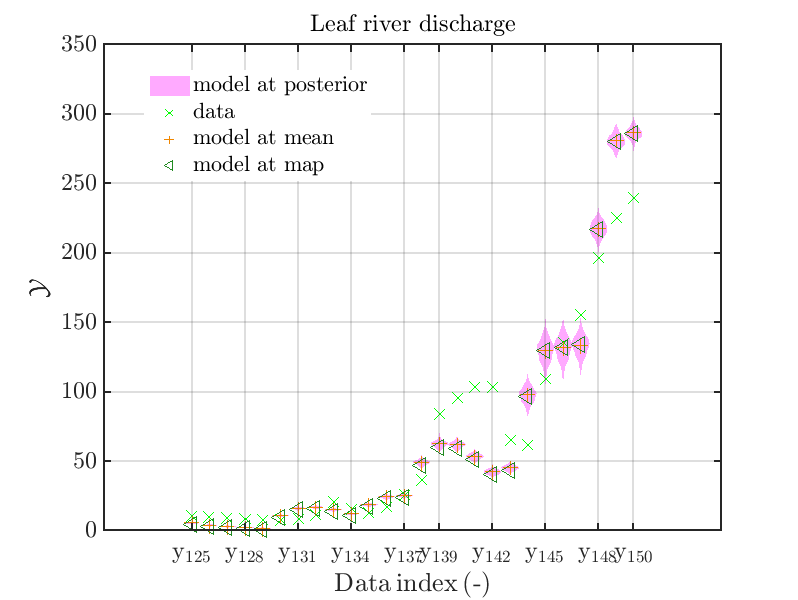
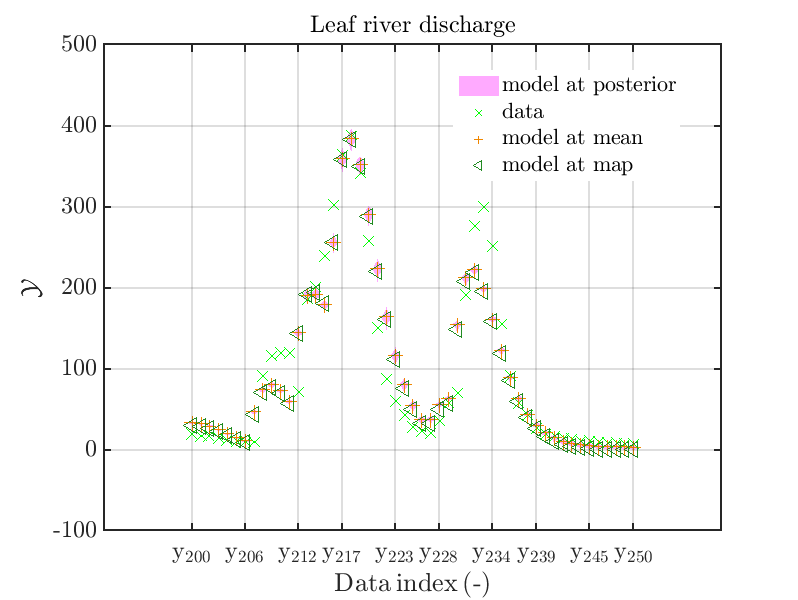
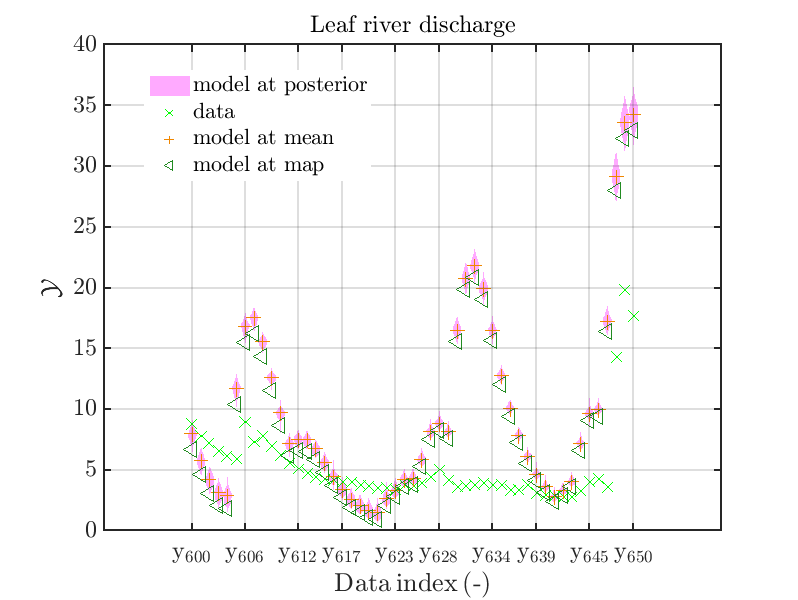
with those above showing the posterior predictive density, one observes that the variation of the posterior predictive values is much larger as the variation of the model outputs.

To inspect this in more detail, one can produce a set of combined plots by the commands

mod_UQLab_plotSeriesPred_2021(mySamples,myData,'post&Model',myPointEstimate,25,50)
title('Leaf river discharge');

mod_UQLab_plotSeriesPred_2021(mySamples,myData,'post&Model',myPointEstimate,125,150)
title('Leaf river discharge');
      
mod_UQLab_plotSeriesPred_2021(mySamples,myData,'post&Model',myPointEstimate,200,250)
title('Leaf river discharge');
   
mod_UQLab_plotSeriesPred_2021(mySamples,myData,'post&Model',myPointEstimate,600,650)
title('Leaf river discharge');

resulting in

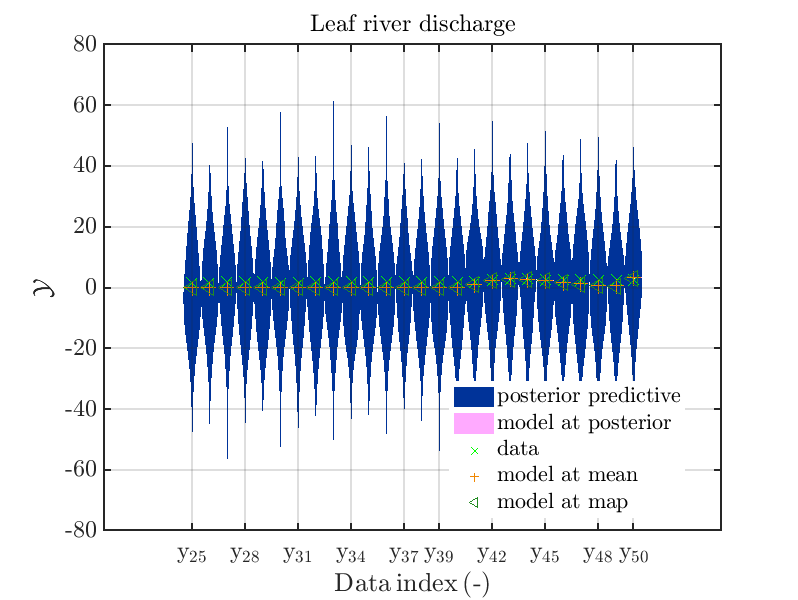
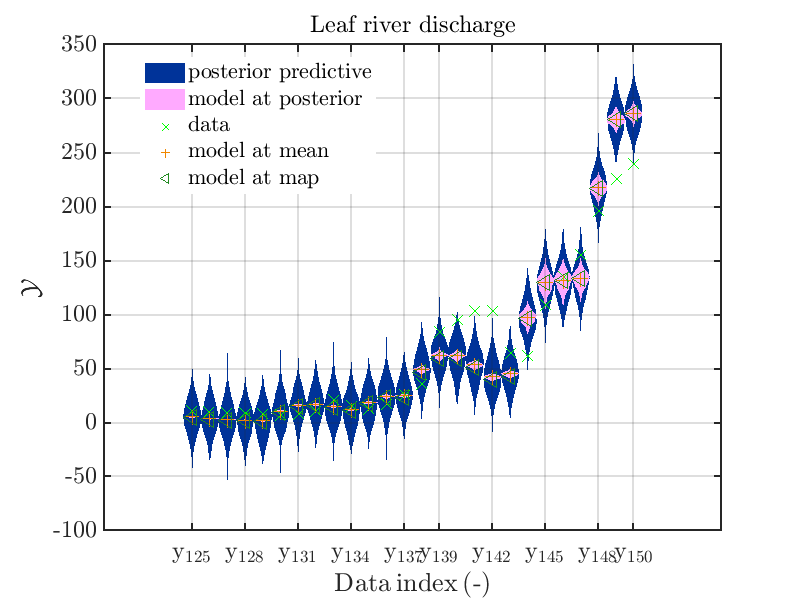
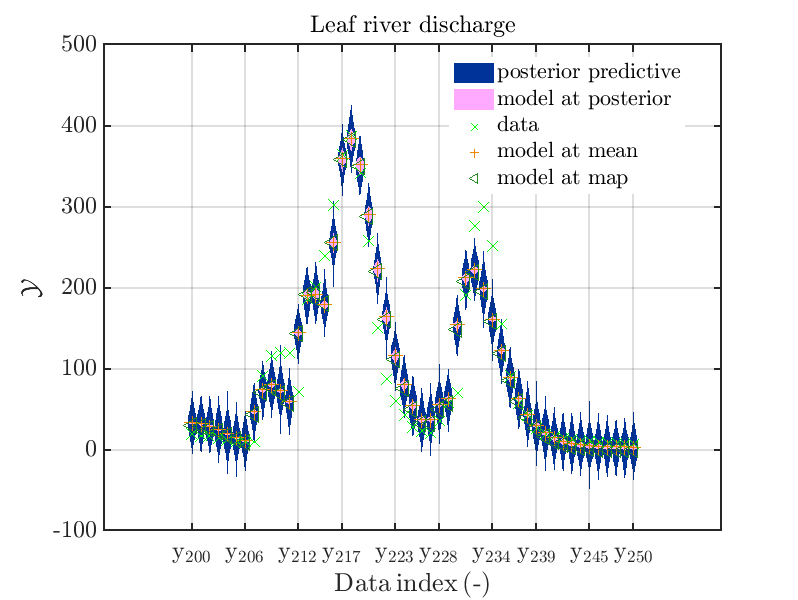
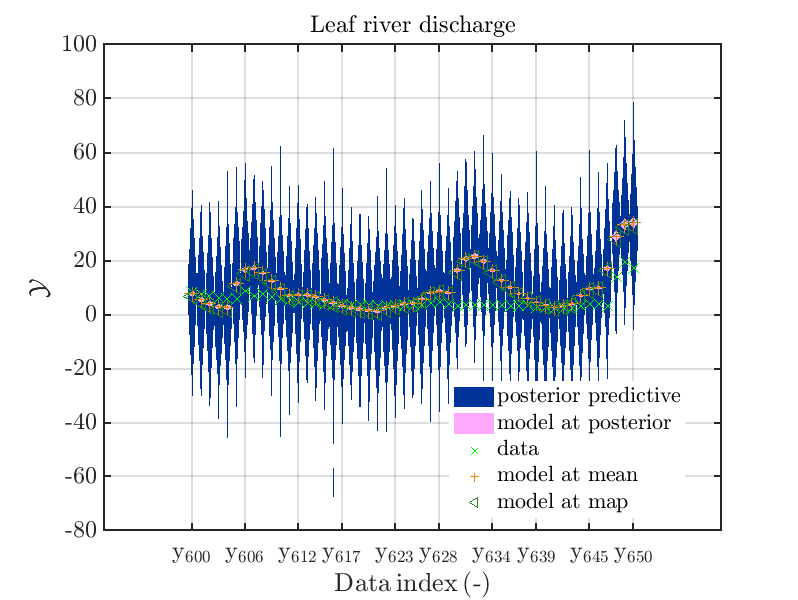
Hence, we see that for many index values the variation of the model output is much smaller then the
variation resulting from the additve noise.

In some of the index value one can only see he density plot for the model output variation by using the zoom in feature of the matlab graphic window, leading for example to

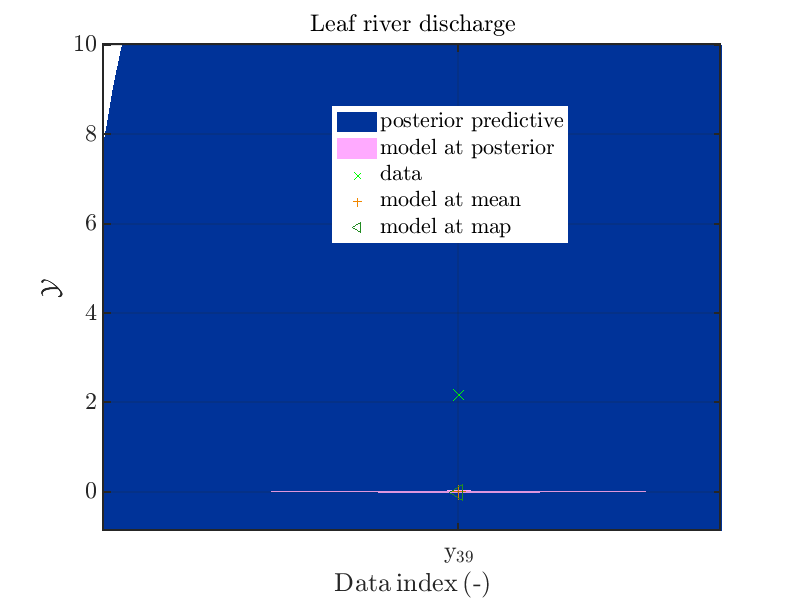
Now, two index ranges are considered such that the size of the model output variation compared
to the variation of the posterior predictive is larger as for other index ranges. To compare for those ranges the posterior predictive distribution, which interpreted as the output of a (full) forward UQ using the computed posteriori density, with the result of the simplified forward UQ, i.e. adding appropriate noise values to the model output at the mean point estimate, one can create these
for the first data sets plots with the commands

mod_UQLab_plotSeriesPred_2021(mySamples,myData,'post&Model',myPointEstimate,144,152)
title('Leaf river discharge - full forward UQ');

mod_UQLab_plotSeriesPred_2021(mySamples,myData,'Model(PE)+noise',myPointEstimate,144,152)
title('Leaf river discharge - simplified forward UQ');

mod_UQLab_plotSeriesPred_2021(mySamples,myData,'post&Model(PE)+noise',myPointEstimate,144,152)
title('Leaf river discharge - full and simplified forward UQ');

mod_UQLab_plotSeriesPred_2021(mySamples,myData,'post&Model(PE)+noise:edges',myPointEstimate,144,152)
title('Leaf river discharge - full and simplified forward UQ');

one gets the plots

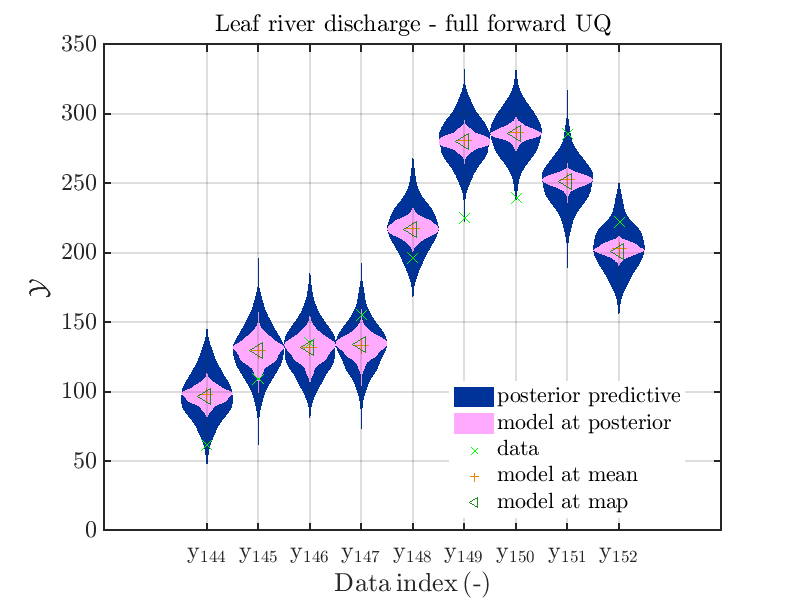
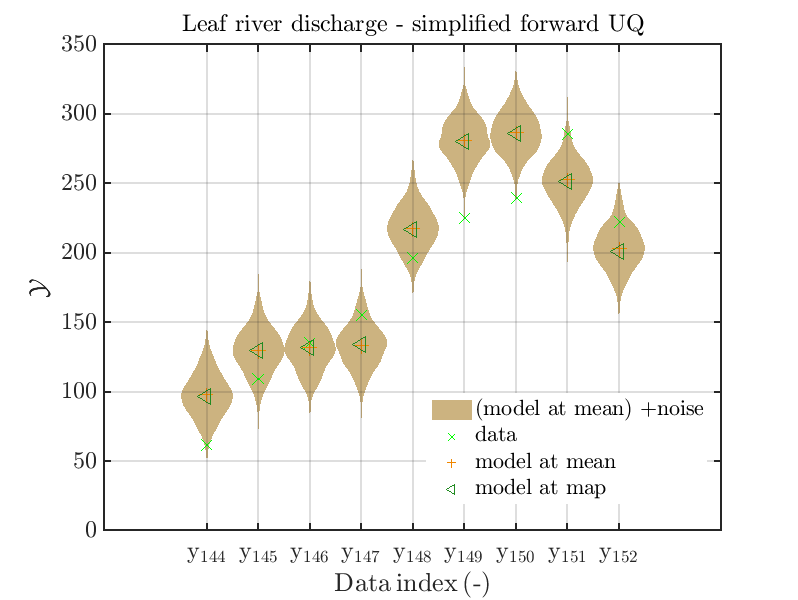
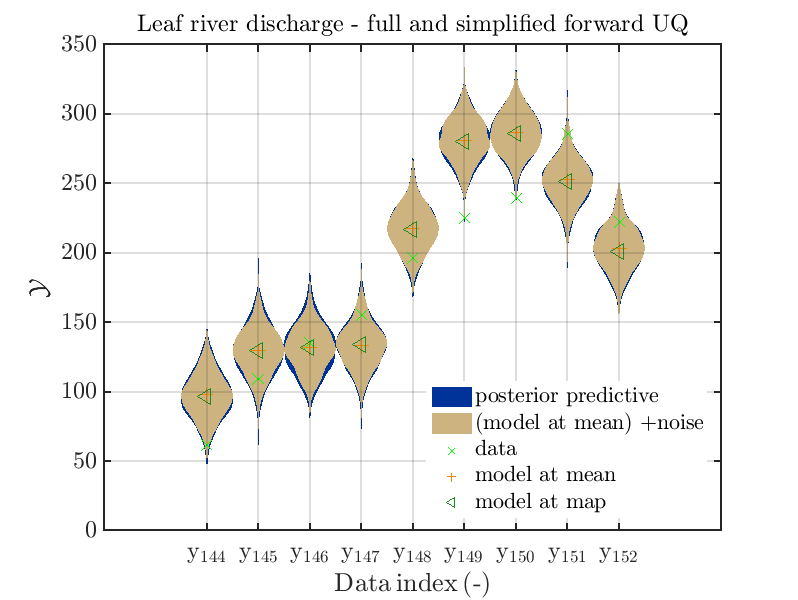
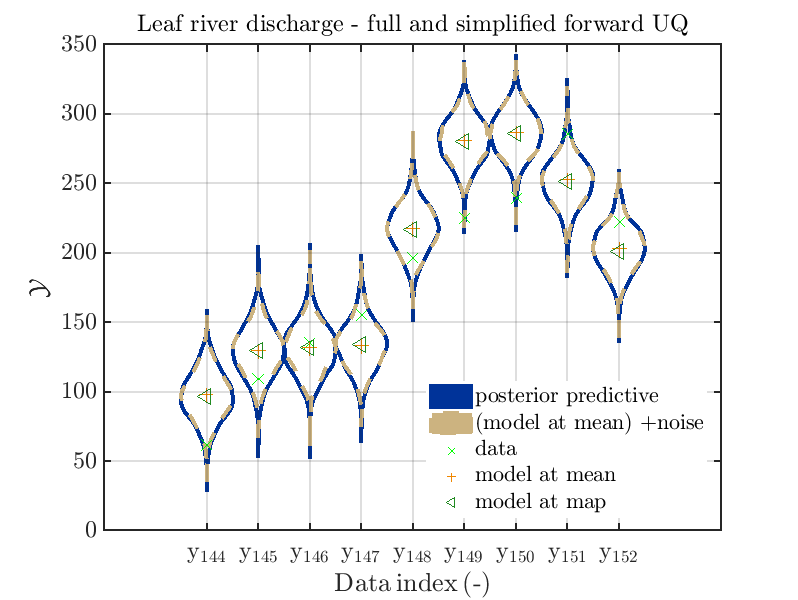
Considering some other data range and using

mod_UQLab_plotSeriesPred_2021(mySamples,myData,'post&Model',myPointEstimate,215,235)
title('Leaf river discharge - full forward UQ');

mod_UQLab_plotSeriesPred_2021(mySamples,myData,'Model(PE)+noise',myPointEstimate,215,235)
title('Leaf river discharge - simplified forward UQ');

mod_UQLab_plotSeriesPred_2021(mySamples,myData,'post&Model(PE)+noise',myPointEstimate,215,235)
title('Leaf river discharge - full and  simplified forward UQ');

mod_UQLab_plotSeriesPred_2021(mySamples,myData,'post&Model(PE)+noise:edges',myPointEstimate,215,235)
title('Leaf river discharge - full and  simplified forward UQ');

one gets

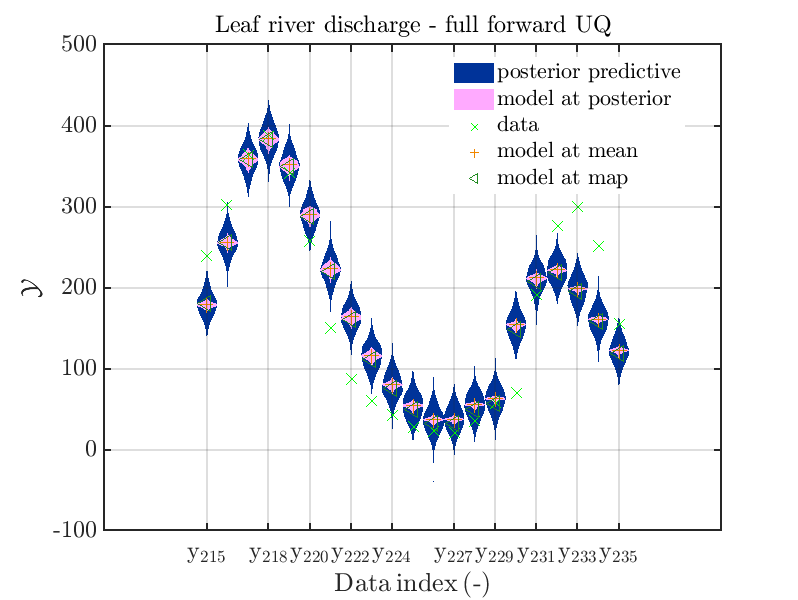
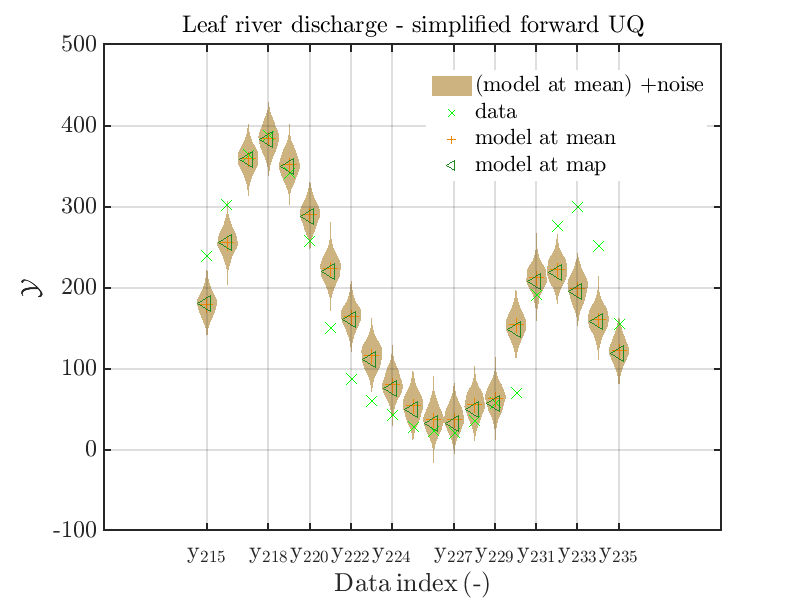
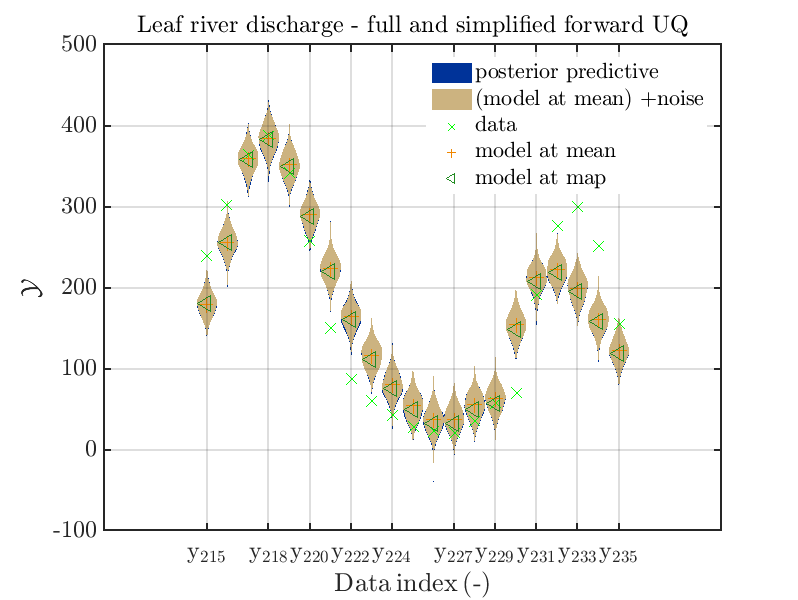
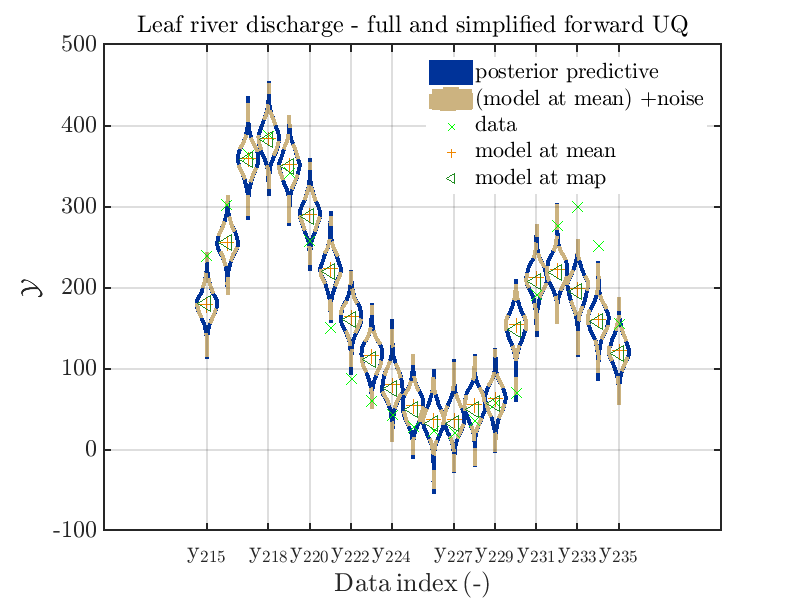
In view of the above result one can deduce that it may be sufficient to perform a simplified forward UQ to derive new predictions for the Leaf river discharge, or one may switch between the simplified forward UQ and the full forward UQ depending on the computed value for of the discharge.

Predator-prey model calibration

Considering the predator-prey model calibration as in https://www.uqlab.com/inversion-predator-prey one can use the commands

uq_Example_Inversion_04_PredPrey

% Using the UQLab Modules 1.4.0 feature to deal with Mean and MAP point estimate at the same time
uq_postProcessInversion(myBayesianAnalysis,...
                        'badChains', badChainsIndex,...
                         'pointEstimate',{'Mean','MAP'},.....
                        'prior', 1000,...
                        'priorPredictive', 1000,...
                        'posteriorPredictive', 1000);

% Extract data from myBayesianAnalysis and copy them to local variables to be used as
% input for mod_UQLab_plotSeriesPred_2021
myData = myBayesianAnalysis.Data
DataTest = myBayesianAnalysis.Data
mySample = rmfield(myBayesianAnalysis.Results.PostProc.PriorPredSample,'Prior');
mySample(1).PostPred= myBayesianAnalysis.Results.PostProc.PostPredSample(1).PostPred
mySample(2).PostPred= myBayesianAnalysis.Results.PostProc.PostPredSample(2).PostPred
mySample(1).Post= myBayesianAnalysis.Results.PostProc.PostPredSample(1).Post
mySample(2).Post= myBayesianAnalysis.Results.PostProc.PostPredSample(2).Post
myPointEstimate = myBayesianAnalysis.Results.PostProc.PointEstimate.ForwardRun

% start of plot creation
mod_UQLab_plotSeriesPred_2021(mySample(1),myData(1),'post&Model',...
    myPointEstimate);
title('Hare data - full forward UQ')

mod_UQLab_plotSeriesPred_2021(mySample(1),myData(1),'Model(PE)+noise',...
    myPointEstimate)
title('Hare data - simplified forward UQ')

mod_UQLab_plotSeriesPred_2021(mySample(1),myData(1),'post&Model(PE)+noise',...
    myPointEstimate)
title('Hare data - full and  simplified forward UQ')

mod_UQLab_plotSeriesPred_2021(mySample(1),myData(1),'post&Model(PE)+noise:edges',...
    myPointEstimate)
title('Hare data - full and  simplified forward UQ')

The final commands produce for the hare data a plot showing the combination of the posterior predictive distribution, which can be interpreted as the result of a full forwards UQ computation of the densities derived by the result of the performed inverse UQ and of the model output variation showing the result of the simplified forward UQ using the model output at the mean of posterior density, see

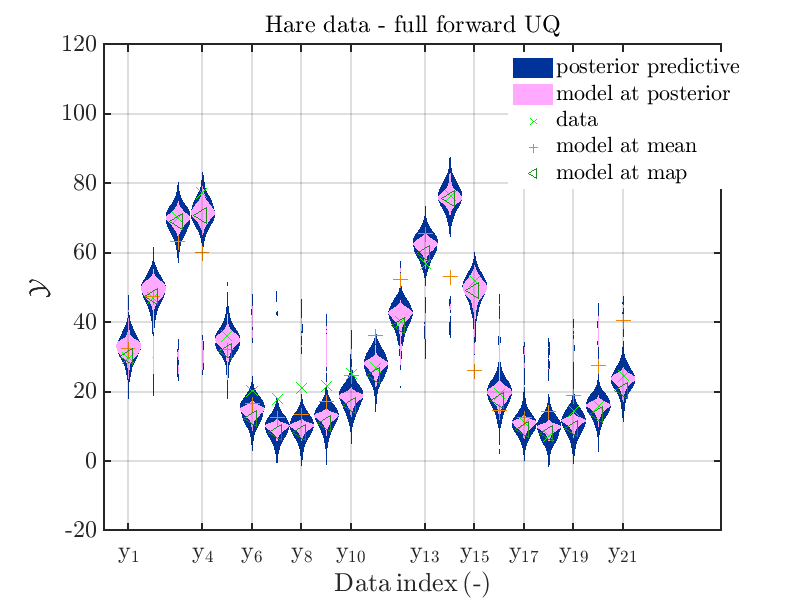
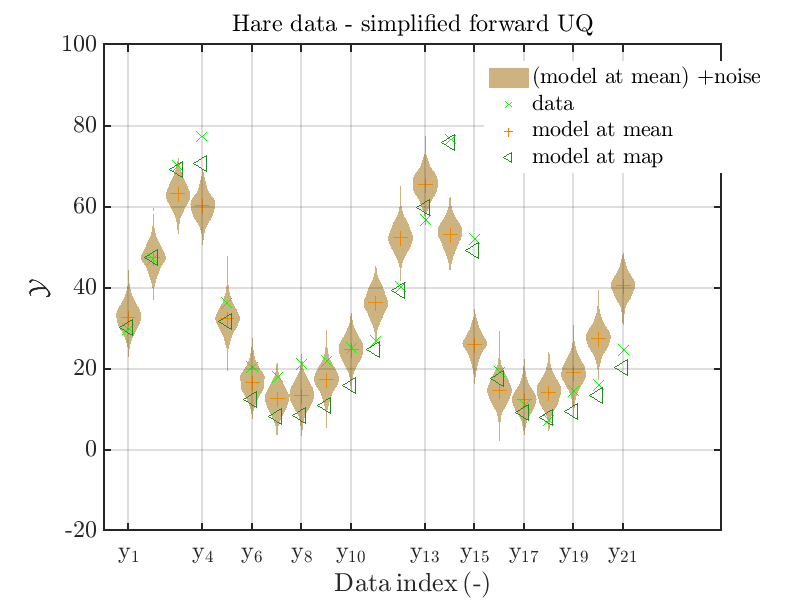
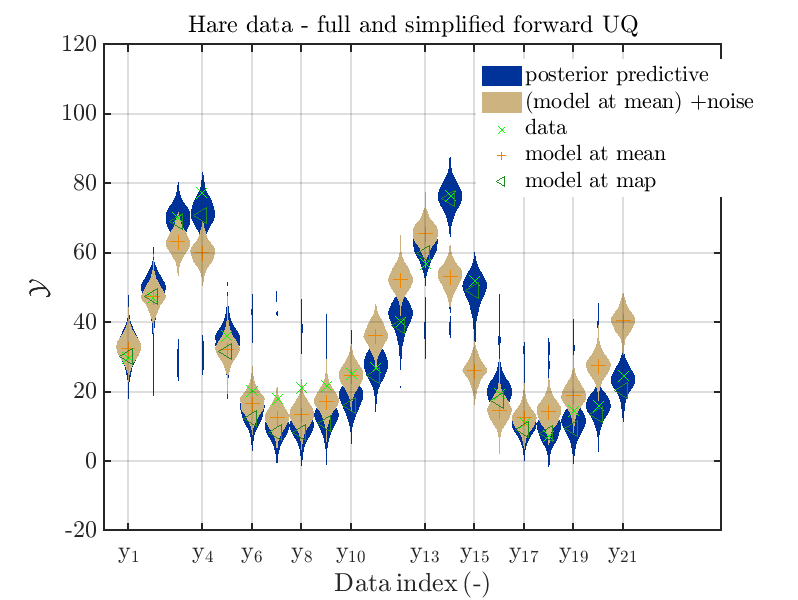
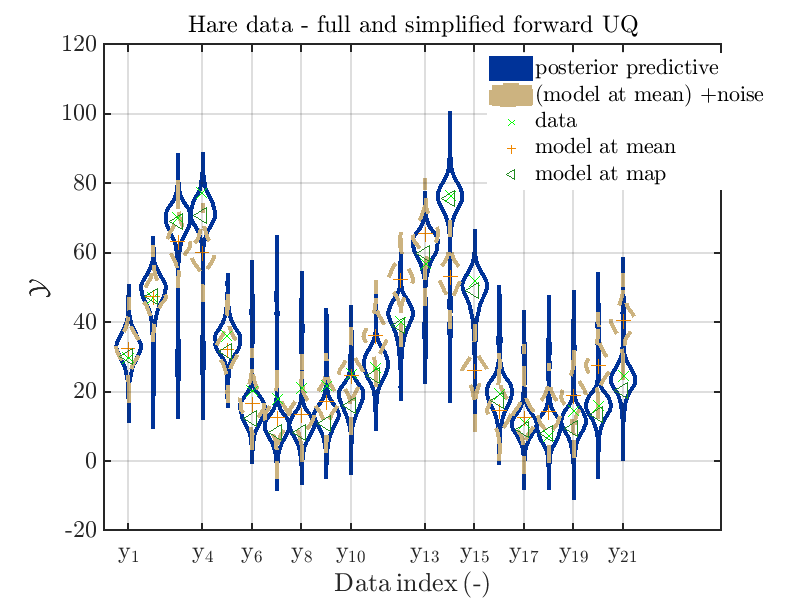
Hence, here one can observe that quite often the variations of the model output are of the same order as the variations of posterior predictive distribution. Moreover comparing the results for the hare data at the indices 3,4, 10, 11, 12, 14, 15, 16, 19, 20, 21 it is obvious that the results one can get from the simplified forwards UQ computation using the model output at the mean is not appropriate to approximate the results of the full forward UQ computation.

Moreover, a similar set of plots is created for the lynx data, using the commands

mod_UQLab_plotSeriesPred_2021(mySample(2),myData(2),'post&Model',...
    myPointEstimate);
title('Lynx data - full forward UQ')

mod_UQLab_plotSeriesPred_2021(mySample(2),myData(2),'Model(PE)+noise',...
    myPointEstimate)
title('Lynx data- simplified forward UQ')

mod_UQLab_plotSeriesPred_2021(mySample(2),myData(2),'post&Model(PE)+noise',...
    myPointEstimate)
title('Lynx data- full and simplified forward UQ')

mod_UQLab_plotSeriesPred_2021(mySample(2),myData(2),'post&Model(PE)+noise:edges',...
    myPointEstimate)
title('Lynx data- full and simplified forward UQ')

is leasing to the plots

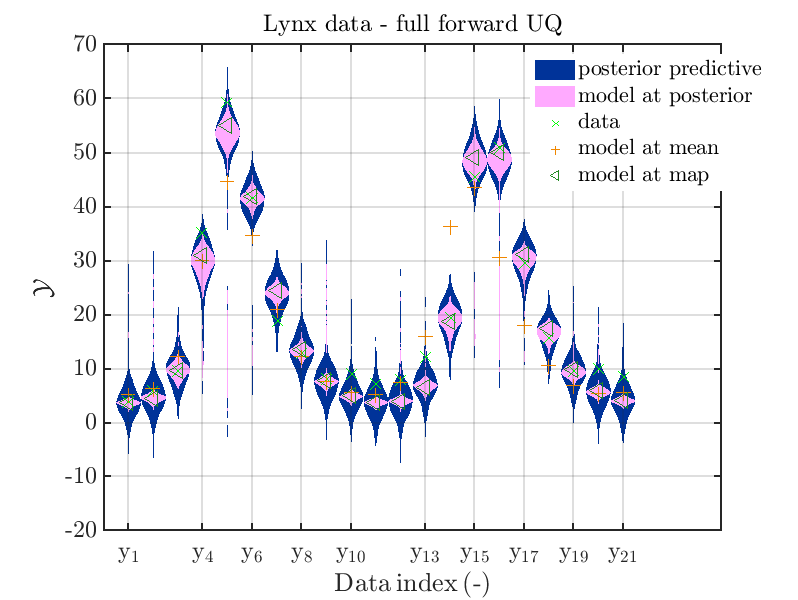
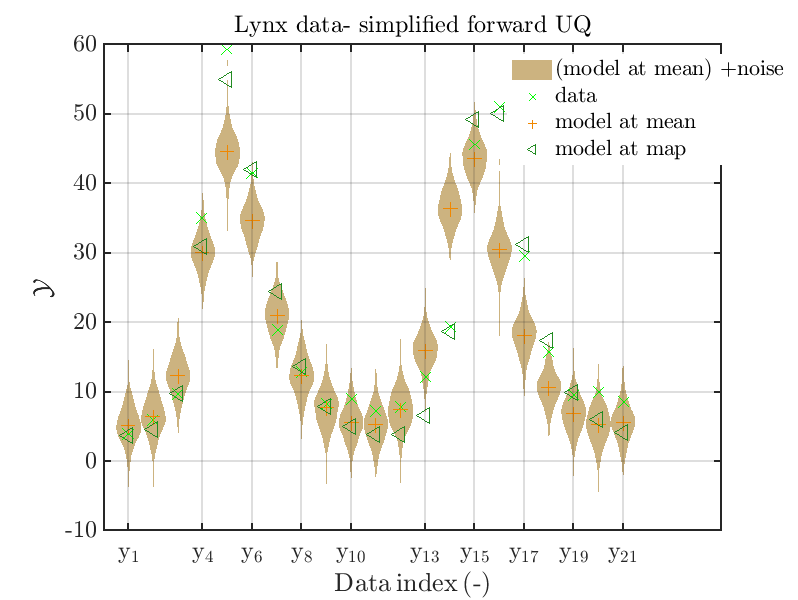
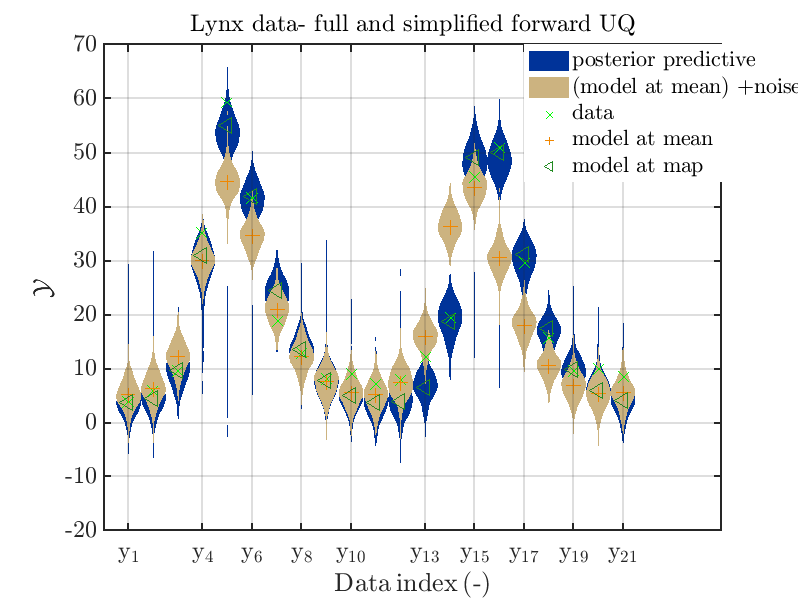
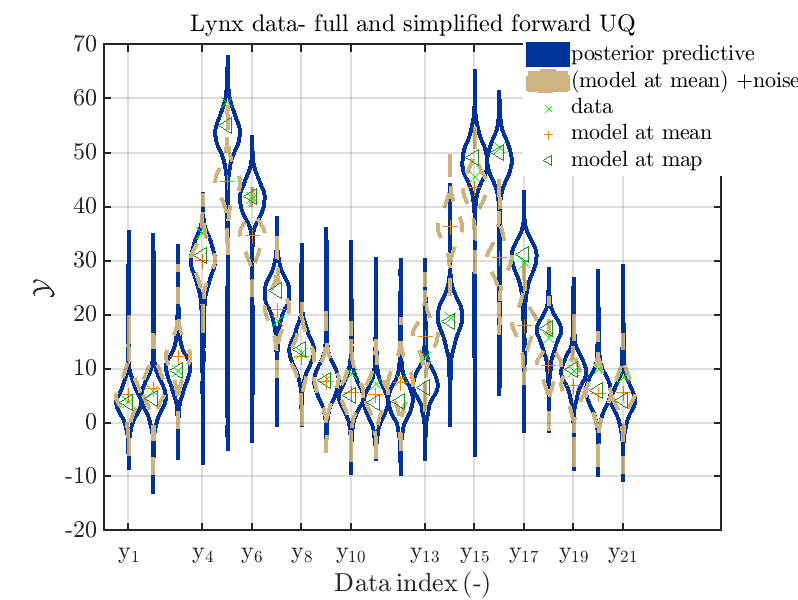
Hence, here one can observe that also for the lynx data quite variations of the model output are quite often of the same order as the variations of posteriori predictive distribution. Moreover comparing the results f for the lynx data at the indices 5, 6, 13, 14, 16, 17, 18 it is obvious that the results one can get from the simplified forwards UQ computation using the model output at the mean is not appropriate to approximate the results of the full forward UQ computation.

To get plots such that the model evolution at the mean of the posteriori density is replaced by the model evolution at the MAP point estimate, one has to perform the following commands:

uq_postProcessInversion(myBayesianAnalysis,...
                        'badChains', badChainsIndex,...
                        'prior', 1000,...
                        'priorPredictive', 1000,...
                        'posteriorPredictive', 1000,...
            'pointEstimate','MAP');
                    
% Update sample value to keep consistency   
myMapData = myBayesianAnalysis.Data

myMapSample = rmfield(myBayesianAnalysis.Results.PostProc.PriorPredSample,'Prior');
myMapSample(1).PostPred= myBayesianAnalysis.Results.PostProc.PostPredSample(1).PostPred
myMapSample(2).PostPred= myBayesianAnalysis.Results.PostProc.PostPredSample(2).PostPred
myMapSample(1).Post= myBayesianAnalysis.Results.PostProc.PostPredSample(1).Post
myMapSample(2).Post= myBayesianAnalysis.Results.PostProc.PostPredSample(2).Post
myMapPointEstimate = myBayesianAnalysis.Results.PostProc.PointEstimate.ForwardRun       

% plot posteriori predictive density and model output density for 
%  hare data 10,...,20 

mod_UQLab_plotSeriesPred_2021(myMapSample(1),myMapData(1),'post&Model(PE)+noise',...
    myMapPointEstimate)
title('Hare data - full and simplified forward UQ (MAP)')

mod_UQLab_plotSeriesPred_2021(myMapSample(1),myMapData(1),'post&Model(PE)+noise:edges',...
    myMapPointEstimate)
title('Hare data - full and simplified forward UQ (MAP)')



mod_UQLab_plotSeriesPred_2021(myMapSample(2),myMapData(2),'post&Model(PE)+noise',...
    myMapPointEstimate)
title('Lynx data- full and simplified forward UQ (MAP)')


mod_UQLab_plotSeriesPred_2021(myMapSample(2),myMapData(2),'post&Model(PE)+noise:edges',...
    myMapPointEstimate)
title('Lynx data- full and simplified forward UQ (MAP)')

Considering the resulting plots

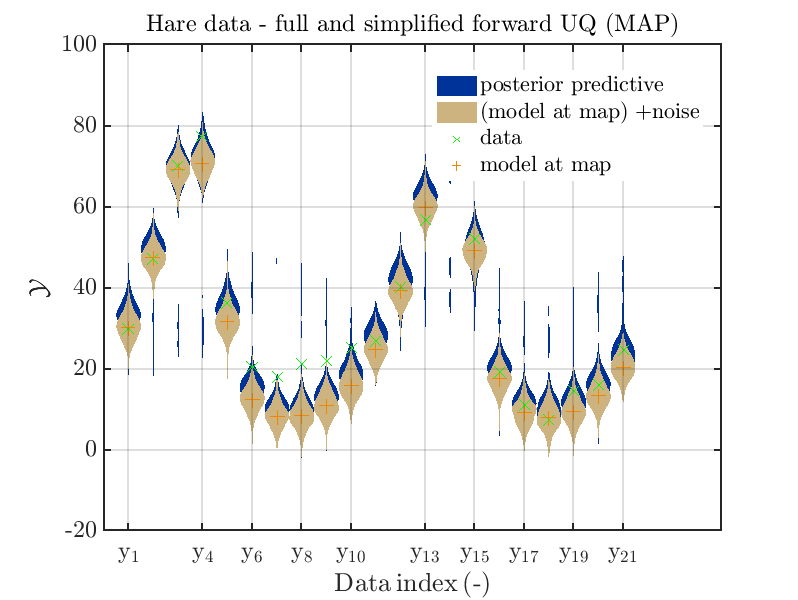
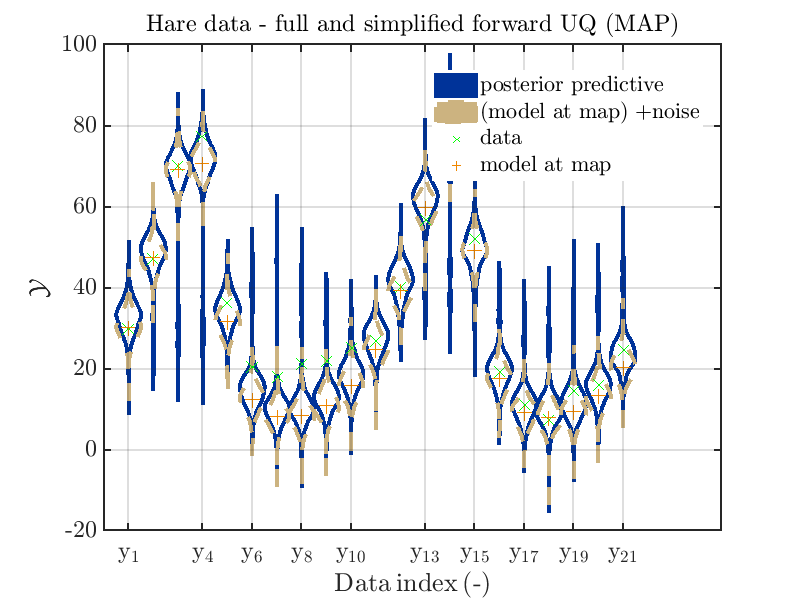
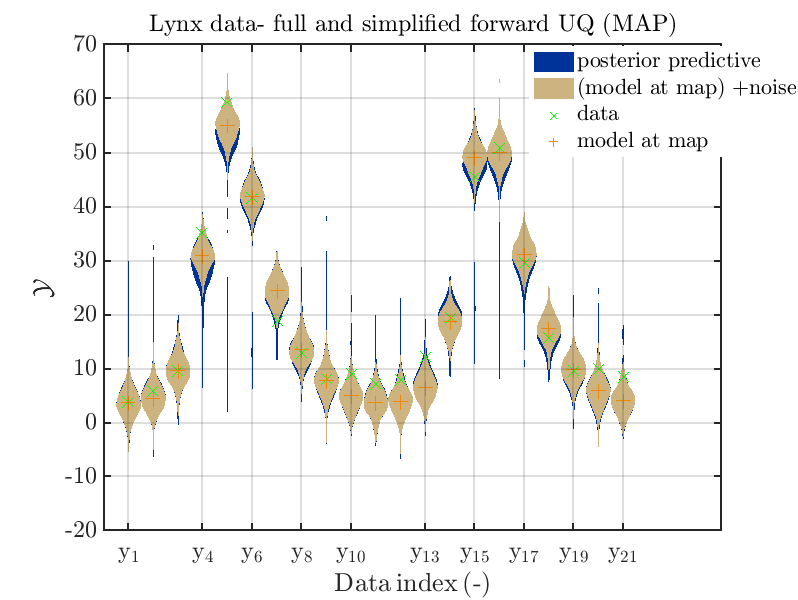
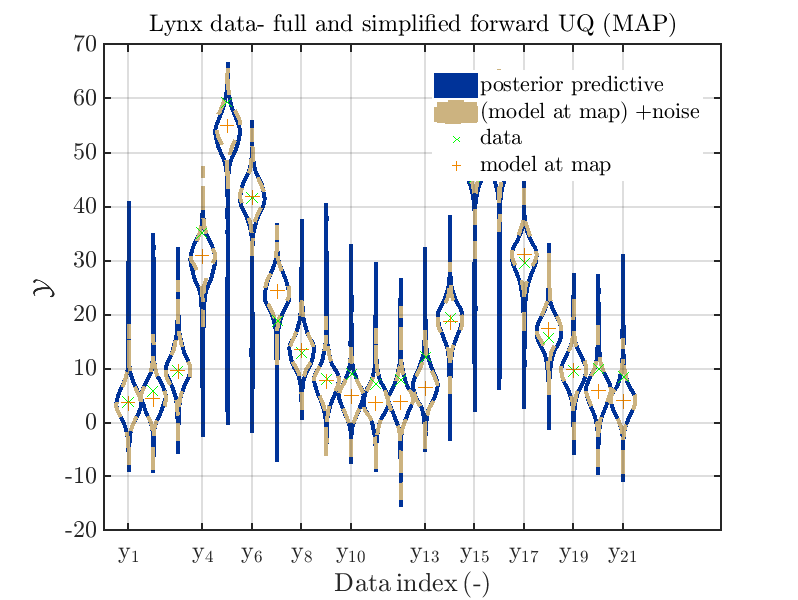
we see that changing to the MAP estimate as improved the result of the simplified forward UQ computations, but considering the hare data at the indizies 1,2,5,10,11,12,13 21,
the lynx data at the indizes 4 , and the missing rare events in the simplified forward Uq results yields that changing to the MAP point estimate has improved the approximation but the results of the simplified forward UQ are still not sufficient to suggest to use the simplified forward UQ for further considerations.

Greetings
Olaf

[paulremo (Paul-Remo Wagner)]

Hi @olaf.klein

Thank you for providing the modified plotting function and this very clear post. There are some features here that definitly belong to the next version of the Bayesian module, which is still a couple of months away due to the recent release of v1.4. Particularly, I think the indexing range feature and the switch to a more easily distinguishable point-estimator marker (e.g. triangle) is very high on the priorities list.

I quite like your idea of offering more flexibility to the user for deciding what to put in the plots. Perhaps, a more UQLab way would be to allow the 'predDist' name-value pair in uq_display_uq_inversion, which produces the predictive plots, to accept an options structure myPredDistOpts instead of just a logical.

myPredDistOpts could then be filled with all kinds of options and combinations such as

myPredDistOpts.Range = [1:10, 200:210];
myPredDistOpts.Sample.Post = true;
myPredDistOpts.Sample.Prior= true;
myPredDistOpts.Sample.PostPred = true;
myPredDistOpts.Sample.PriorPred = false;

These would then be considered for the plot upon calling

uq_display(myBayesianAnalysis, 'predDist', myPredDistOpts)

What do you think?

[olaf.klein]

Hi @paulremo, (Hello also to anyone else who is interested in this topic)

Thanks for your support and for your suggestions.

I like the idea of using a name-value pair as parameters for uq_display_uq_inversion to allow
some changes in the plots without requiring further calls of uq_postProcessInversion, but
there are some issues one needs to decide/consider before it can be implemented:

1. Are your examples supposed to be
   a) options related only to the plots activated/deactivated in the current UQLab implementation by the ‘‘predDist’’ flag, and maybe the new plots suggested in my post, or
   b) option for all plot types generated by uq_display_uq_inversion?
   The answer a) fits to the name of the option and the name of the name for the local variable in your example, but in addition to myPredDistOpts.Sample.PostPred there is also a flag
   myPredDistOpts.Sample.Post, seeming to be a switch for activating/deactivating the generation of the scatter plot for the posterior density, Hence, it seems to me that you may had somehow the situation b) in mind when writing your example, at least subconsciously.
   But, if you really want to use the ansatz in b), I suggest to change the name for the name-value pair, and of the variable in the discussion, e.g. replacing 'PredDist' by the a new name, like e.g. 'plotOpts' or 'dispOpts'. Moreover, I would suggest to denote flags for scatter plots by Scatter . Hence, myPredDistOpts.Sample.Post may be replaced by myPlotOpts.Scatter.Post.
   But, i must admit that I do not know, what could be good common start for the options related to the plots generated by mod_UQLab_plotSeriesPred_2021.m and and plotSeriesPred.m i.e.
   for 'PostPred', 'PriorPred', 'Model' or 'ModelAtPost', 'Model(PE)+noise', or
   'Model(PE)+noise:edges' (see below).
   (Side remark: I have now performed many Bayesian Inversions using UQLab without being interested in the prior scatter plot. Here, it became my habit to simply ignore the
   created scatter plot for the prior, and I think that in general I would be to lazy to stop the
   creation of this plot by using some flag/parameter in the code. But maybe other users would like
   to use this flag, and even I may like to use it if I perform that many Bayesion inversion in one program run such that the number of created windows may become to large, i.e. larger then 100–120, and could maybe force a freze of matlab or of my whole laptop. )

2. It is my interpretation of your example that you suggest to use flags to activate/deactivate the possible plots components in a new version of plotSeriesPred.m that is using parts of mod_UQLab_plotSeriesPred_2021.m. If this interpretation is correct, one has to think on the order of the creating of the plots, such that hiding of interesting parts is reduced:
   I think that a good order of plots would be
   1.'PriorPred': plot of prior predictive density, i.e. (model output at priori samples) + noise,
   2.'PostPred': plot of posterior predictive density, i.e. ( model output at posterior samples) + noise,
   3.'Model(PE)+noise': plot of (model output at point estimate) + noise,
   4. ’Model' or ' ModelAtPost': plot of model output at posterior samples ,
   5.'Model(PE)+noise:edges': plot of boundary of violin plot for (model output at point estimate) + noise region, now shown with an connected line.
   (This is supposed to be typically combined with the 'PostPred' Plot, such that one can compare the result of (full) forward UQ and simplified forward UQ.

3. If myPredDistOpts.Range = [1:10, 200:210]; indicates to replace my StartInd and EndInd input values leading to the plot range StartInd,…, EndInd by a more general set of numbers as plot range, one has to change some parts of the code in mod_UQLab_plotSeriesPred_2021.m that make use on the current form of the plot range.
   Moreover, one should spend some time on considering to update the generation of tic and of the tic numbers at the x axis, if one is allowing general points sets, like, e.g. [1,3,6,9:11,16,19,20,23,25,42,45,47,48,50,51,70,71,73,79,80,81,84,88,90,93,94]. Currently, maximal 10 numbers are shown, but by counting one can figure out for each ``violin plot’’ the corresponding index. How to deal with a more general situation requires some further consideration.

   Therefore, I think that one has to decide if using the general plot range instead of StartInd,…, EndInd is worth the induced further work and complexity.

4. Moreover, for the plot range one also needs to take into account that there can be multiple data groups such that one needs to define the plat range for each of these groups. To formulate this in way that is correct UQLab style need as least some considerations.

5. In addition, one may have to decide if also a scalar version of the plots 3) – 5) in point 2 is needed, or if is is sufficient to provide the possibility to create of the violin plots also in the case of a scalar model output.
   Examples of the corresponding plots can be generate with my current function
   by

   uq_Example_Inversion_01_Beam
   myData = myBayesianAnalysis.Data
   mySamples.PostPred= myBayesianAnalysis.Results.PostProc.PostPredSample.PostPred
   mySamples.Post= myBayesianAnalysis.Results.PostProc.PostPredSample.Post
   
   myPointEstimate=myBayesianAnalysis.Results.PostProc.PointEstimate.ForwardRun
   
   mod_UQLab_plotSeriesPred_2021(mySamples,myData,'post&Model',myPointEstimate)
   mod_UQLab_plotSeriesPred_2021(mySamples,myData, ...
       'post&Model(PE)+noise:edges', myPointEstimate)
   

leading to the plots

6. Moreover, a further possible parameter may be a field xPos of the length of the data vector such that xPos(i) provides the horizontal position to be used for the center of violin plot for the data point i.
   This could be (a linear transformattion of) the values for some non-UQ input parameter that is evaluated in the model, like e.g. q_i in the Topic: Bayesian inversion for structural parameter identification (the load varies in each measurement ) or the load values in the Topic: Bayesian inference with changing (known) model parameters.

   The generated plots should allow to get some impression of the dependence of the derived results on this non-UQ input parameter. This may require some considerations how to scale the size violin plots in the code, or some considerations/ try and error cyclus for the UQLab-User how to transform to values the non-UQ input parameter to get a plot with violin plots in an appropriate size.

   I created modifications of ‘‘plotSeriesPred.m’’ that are generating this kind of plots, an example is shown below. Since this modification is also an example of dirty coding style, I do not dare to provide it here in its current form.

Scr_extr_UQLab_3rd_combi_reload-fig28.png

7. I created serveral modefications plotSeriesPred.m such that I could use them to
   combine serveral plots into one plot, using the provided like xPos in point 6 combined with
   plot of a subrange using that this function only deal with one plot in one call. To allow this kind of combination in a way that is an appropriate UQLab way may require some work and I do not
   know if anyone else may need this possibility.

Okay, I think this post is already quite long and should provide some possibilities for discussion.

Greetings
Olaf

[olaf.klein]

Hi @paulremo, (Hello also to anyone else who is interested in this topic)

trying to follow your suggestion in your post in the topic Uq_display_uq_inversion: Determine limits for scatter plots for posteriori samples from the posteriori samples instead of using prior sampesl I would like to present a further possible flag for the scatter plots:
One should add a flag like ‘scatter.reusePriorLimits’ or ‘scatter.useDifferentLimits’ that could allow to switch between:

• Using the extrema of the samples for the prior density to determine the limits for the scatter plots for the prior and the posterior density, such that one can visualize the information gain thanks to the performing the Bayesian inversion.
• Using the extrema of the samples for the posterior density to determine the limits for the scatter plots for the posterior density (and the extrema of the samples for the prior density to determine only the limits for the scatter plots for the prior) such that one is able to really inspect the features of the posterior density in the posterior scatter plot in the case of a large information gain.

Greetings
Olaf