Hello all,
Firstly, I wanted to thank you for the UQLAB package and this community,
I’m a newcomer to the field of Bayesian inversion, and I’ve been experimenting with the “multiple model outputs” example in the section 2.3 of Bayesian user manual (the process of calibrating a beam parameters based on beam deflection at different spans) trying to to improve my understanding of the entire process.
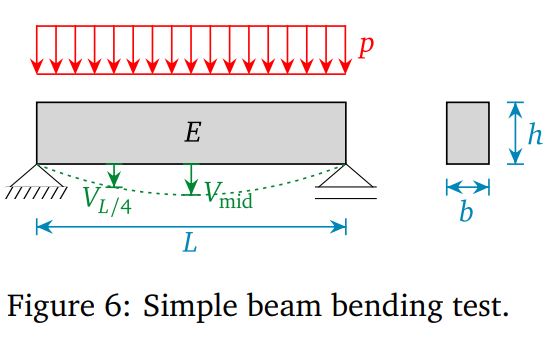
At first, I made some artificial deflection data based on fixed values of (b,h,p) and variability in (E,L). the Young’s Modulus values(E) are sampled from a normal distribution with a mean value and standard deviation of 50 (GPa) and 4.5 (GPa) respectively. While in the original example the beam length (L) was considered as a fixed value, I’ve considered it to follow a normal distribution with a mean value and standard deviation of 5 (m) and 0.1 (m) respectively.
A noise term sampled from a normal distribution (mean=0 , std dev = 0.5 (mm)) has been added to the artificial deflection data as well.
I ran two models, one with an informative prior and another one with a non-informative prior
informative prior (UQ_main_Informative.m):
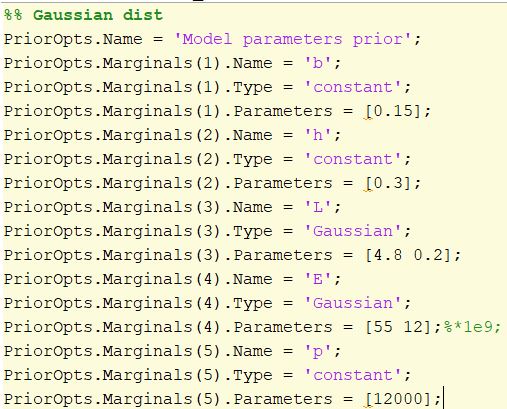
non-informative prior (UQ_main_nonInformative.m):
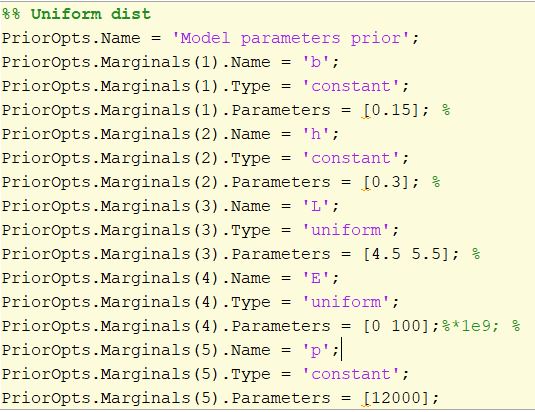
To reduce the number of calibrated model parameters, I’ve considered a fixed discrepancy parameter in both cases with a sigma2= 0.25 (have I chose it correctly based on the std dev of the imposed white noise ?)
according to the discussions I’ve read on here on the convergence check for MCMC, I’ve also increased the MCMC.steps to 1000 to maintain a MPSRF value below 1.1 (MPSRF=1.08).
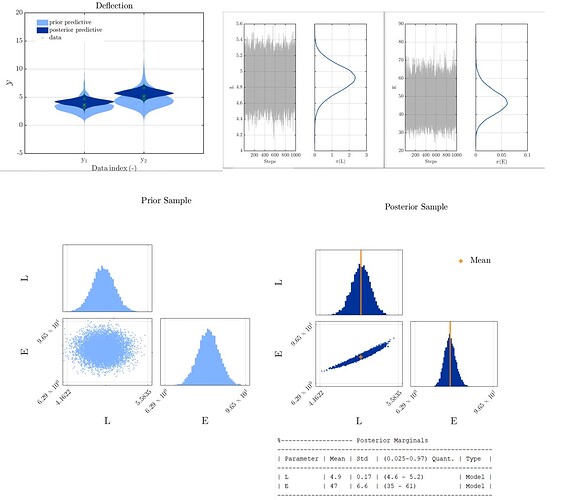
Below you can find the output I get from the model with informative prior function (UQ_main_Informative.m):
While the posterior mean that I get from this model matches well (within 10% error) with the expected mean value of the sampled “E” and “L” values, but the posterior std_dev show much more deviation than the expected value. I was wondering if there is anything I can do to reach better agreement between my posterior moments and the expected values?
I have noticed that the correlation between E and L is very close to 1, which was expected as the deflection formula is in the form of L^4/E. I am wondering if this constitutes an “ill-posed inversion problem” and how I could find a solution for it?
Furthermore, I am curious if this issue is related to the problem being an under-constrained inverse problem. If so, how should I determine the appropriate number of deflections at different spans based on the number of calibrated parameters?
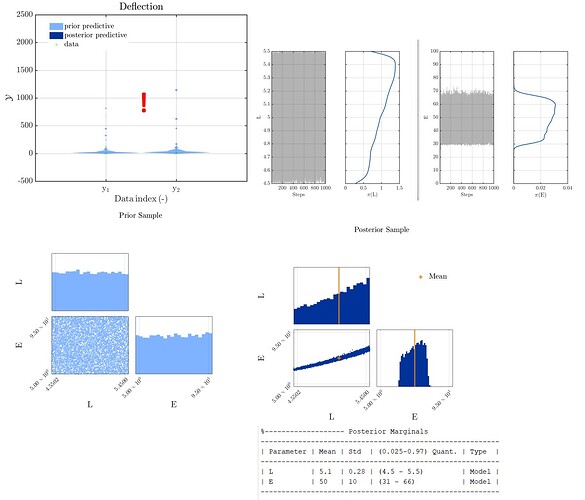
Here’s the output I get from the model with non-informative uniform prior function
(UQ_main_nonInformative.m):
As it could be see, in this case the posterior simply doesn’t look like the expected distribution at all. (is there any way to improve the outcome ?)
I’m sorry for this long post and so many questions, you can find the script and the forward model in here (google drive)
Thanks a lot for your time and consideration in advance,
Mohammad