Hello everybody,
I have computed an orthonormal family of polynomials outside of UQLAB, using just the (empirical estimated) moments from the data I have. I am interested in “plugging-in” this polynomial in UQLAB in order to use PC and PC-Kriging. Is it possible to manually assign this polynomial in UQLAB?
Thanks in advance,
Marius A. Marinescu
URJC University
Hi @marius190,
It is possible to define new polynomial families, but it’s not just “plugging in”. It requires quite a bit of manipulation of the code. Essentially, you would need to define a new PolyType similar to how the PolyType 'fourier' is defined. Is your polynomial family defined explicitly or by recursion coefficients? In the first case, you’ll want to have a look at PolyType 'fourier' and the associated function uq_eval_spectral.m. In the second case, look at any of the standard polynomial families and uq_poly_rec_coeffs.m. The recursion coefficients are assigned at the very bottom of uq_PCE_initialize_process_basis.
UQLab also always includes an isoprobabilistic transform to the associated standard marginals (e.g. in order to use Hermite polynomials, the input is mapped to \mathcal{N}(0,1)). This transform defined in uq_poly_marginals.m. It is used in uq_PCE_initialize.m, l. 229 to define the internally used input. You would need to define here the distribution that the polynomials are orthogonal to (for which you would probably need to define a custom distribution, too), or specify the identity mapping and make sure that you only ever use this polynomial family with the appropriate input data.
However, it might be easier to let UQLab compute the orthonormal family of polynomials associated to your input data by using arbitrary PCE. I saw that you already answered another user’s question about arbitrary PCE so you are well aware of them. What is the reason that you don’t want to use UQLab’s arbitrary polynomials, are they different from what you computed?
But yes, once you have defined your own polynomial family, you can do anything you like with UQLab, including PCE and PC-Kriging. Good luck, and let us know how you deal with it! 
Hi @nluethen,
I appreciate your detailed answer. I will try to adapt the code. The reason is that arbitrary PCE in UQLAB, as far as I understood, need a well-defined probability distribution. I only have data without more knowledge about the distribution and I want to apply the following methodology:
specifically formula (19) and (20). In this paper, they also use the well-know three-term recurrence formulation to compute the orthogonal polynomials. The difference with UQLAB is that, in spite of using the Stieltjes procedure to construct the polynomials (coefficients) having a probability measure, they just use the moments of the random variable without further assumption on the distribution. To illustrate the method, consider a sample of 1000 standard gaussian (pseudo) random numbers. Applying this procedure I get the following first four polynomial bases that match the ones expected, the first four probabilistic Hermite polynomials:
Hi Marius,
I see, makes sense. Yes, arbitrary PCE in UQLab needs an input distribution, and uses the Stieltjes procedure.
My colleagues computed arbitrary PCE from data using a kernel density estimate of the inputs (see Torre et al 2020, Section 2.3.2) with good results on standard machine learning examples. They also comment that computing higher-order moments accurately from data needs a lot of samples, which might limit the applicability of moment-based PCE. So it will be extra interesting what results you will get with SAMBA. Please let us know eventually what you find! You are of course also very welcome to share your code here 
Hi @nluethen ,
Thanks for the answer. The paper looks interesting. I will share in the post if any remarkable result is found
As promised I share here a performance test of aPC throught the method of moments available in the paper “SAMBA” against UQLAB aPC. With UQLAB aPC I mean to apply kernel estimation of the input marginals and Stieltjes procedure for the coefficients of the polynomials. Surprisingly, at least for one dimension, SAMBA and UQLAB have the same performance in terms of the so-called Normalized empirical error:
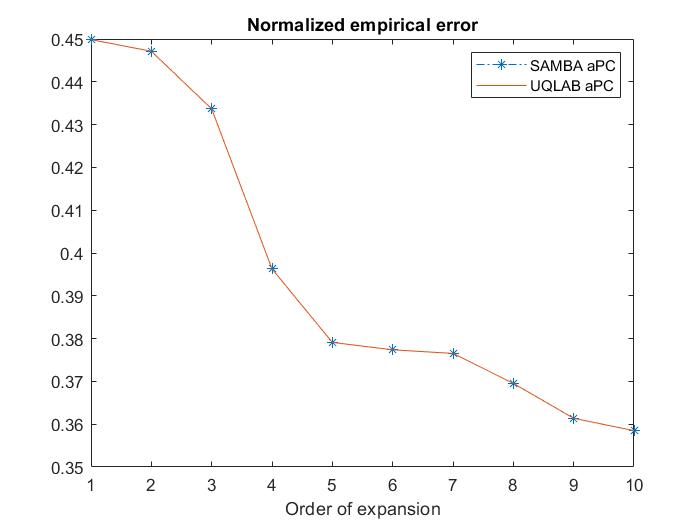
As can be seen in the attached code an picky input random variable is chosen and no less picky Y=M(X):
% Input X | Experimental design
ber= binornd(1,0.5,n,1); % Bernoulli rv
X=normrnd(0,3,n,1).*ber + (1-ber).*normrnd(5,1,n,1).^2+ ...
5*sin( rand(n,1)*2*pi );
% Output Y | Experimental design
Y=exp(-abs(X))+sin(-X)+log(abs(X)+1);
Complete code ( I can’t attach it since it says “new users can not upload attachments”):
%%%%% aPC expansion: SAMBA vs UQLAB-KS %%%%%
%% Main parameters
clearvars
rng(100,'twister');
n=2e3; % Data size
nVal=1e3; % Validation data size
n_order=10; % Arbitrary Polynomial expansion order
%% Experimental design
% Input X | Experimental design
ber= binornd(1,0.5,n,1); % Bernoulli rv
X=normrnd(0,3,n,1).*ber + (1-ber).*normrnd(5,1,n,1).^2+ ...
5*sin( rand(n,1)*2*pi );
% Output Y | Experimental design
Y=exp(-abs(X))+sin(-X)+log(abs(X)+1);
% Validation sets
XVal=linspace(min(X), max(X), nVal)';
YVal=exp(-abs(XVal))+sin(-XVal)+log(abs(XVal)+1);
%% aPC: UQLAB vs SAMBA Moments PC (non sparse version)
syms x
Ypc=zeros(1,n); YpcVal=zeros(1,nVal);
samba_er=zeros(1,n_order); uq_erVal=zeros(1,n_order);
uq_er=zeros(1,n_order);
for p=1:n_order
%% Samba
Pn=sPC_poly(X,p);
Pn_fun=matlabFunction(Pn);
A=zeros(n,p+1);
for i=1:n
A(i,:)=Pn_fun(X(i));
end
% Regresion
alpha=(A'*A)\(A'*Y);
% Y_hat through SAMBA
for i=1:n
Ypc(i)=sum(alpha'.*Pn_fun(X(i)));
end
samba_er(p)=sum((Y-Ypc').^2)/sum( (Y-mean(Y)).^2 );
% Y_hat through SAMBA
for i=1:nVal
YpcVal(i)=sum(alpha'.*Pn_fun(XVal(i)));
end
samba_erVal(p)=sum((YVal-YpcVal').^2)/sum( (YVal-mean(YVal)).^2 );
%% UQLAB aPC (Kernel estimation of marginals)
InputOpts.Marginals(1).Type = 'KS';
InputOpts.Marginals(1).Parameters = X;
% Create an INPUT object based on the specified marginals:
myInput = uq_createInput(InputOpts);
MetaOpts.Type = 'Metamodel';
MetaOpts.MetaType = 'PCE';
MetaOpts.Method = 'OLS';
MetaOpts.ExpDesign.X=X;
MetaOpts.ExpDesign.Y=Y;
MetaOpts.ValidationSet.X = XVal;
MetaOpts.ValidationSet.Y = YVal;
MetaOpts.Degree = p;
myPCE = uq_createModel(MetaOpts);
uq_er(p)=myPCE.Error.normEmpErr;
uq_erVal(p)=myPCE.Error.Val;
end
%% Error representation
subplot(2,1,1)
plot(1:n_order,samba_er,'-.*',1:n_order,uq_er)
xlabel('Order of expansion')
title('Normalized empirical error TRAIN')
legend('SAMBA aPC', 'UQLAB aPC')
subplot(2,1,2)
plot(1:n_order,samba_erVal,'-.*',1:n_order,uq_erVal)
xlabel('Order of expansion')
title('Normalized empirical error VALIDATION')
legend('SAMBA aPC', 'UQLAB aPC')
indent preformatted text by 4 spaces
Auxiliar function needed for SAMBA methodology:
function [p]=sPC_poly(X,n) % Samba
%% We computes the first 2n moments
M=zeros(n+1,n+1); % Hankel Matrix of moments
m=zeros(1,2*n+1)'; % Moments vector. m(k)= moment k+1
n_x=length(X);
m(1)=1;
for i=1: (n-1)
m(i+1)=sum(X.^i)/n_x;
end
for i=(n: 2*n)
m(i+1)=sum(X.^i)/n_x;
M(:,i-n+1)=m(i-n+1 : i+1);
end
if det(M)<=0
warning(['Determinant of Hankel Matrix:' num2str(det(M))])
end
%% We find the Cholesky descomposition of the Hankel matrix of moments
% and find the coeficientes with the three term recurrence relationship:
R=chol(M);
a=zeros(n,1);
b=zeros(n,1);
a(1)=R(1,2)/R(1,1)-0/1;
b(1)=R(2,2)/R(1,1);
for i=2:n % Order of R matrix: n+1,n+1
a(i)=R(i,i+1)/R(i,i)-R(i-1,i)/R(i-1,i-1);
b(i)=R(i+1,i+1)/R(i,i);
end
% J=diag(a)+diag(b(1:(n-1)),-1)+diag(b(1:(n-1)),1);
syms x
p(1)=sym(1); % Orden 0. Como siempre son ortogonales pol=1 (dFx);
p(2)=(x-a(1))/b(1);
if n>1 % p(i)= pol de orden i-1
% p(3)=(x-a(2))/b(2)*p(2) - b(1)/b(2)*1; % a(j)=a_j. b(j)=b_j
for j=2:n
p(j+1)=(x-a(j))/b(j)*p(j) - b(j-1)/b(j)*p(j-1); % p(j)=phi_{j-1}
end
end