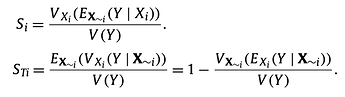I am going through A. Saltelli’s paper [1]. The definition of Sobol first & total indices are given as:
Imagine a model Y=f(A,B,C), i.e. a single output and three inputs. If I am doing a brute-force MC to solve for S_A, and assuming each input has a range of 10 values, then for each of the 10 A values, I’d run a MC varying B,C but keeping A fixed. For each of these runs, I calculate the mean across the N MC runs, then take the variance across these 10 means. This gives me the numerator. The denominator is the variance for an MC run where all inputs are varying.
But am not sure about how to get S_TA (total index for A). Looks like I need to do an MC where only A is variable (B,C fixed), but this would be at each combination of B&C, which is 100 in this example. Thus I get 100 MC runs, take the mean of each then the variance across these means. This gives me the numerator in the second equation.
Is this correct?
[1] Variance based sensitivity analysis of model output. Design and estimator for the total sensitivity index, A. Satelli, et. al., Computer Physics Communications 181 (2010) 259–270.