Transformation between X and U domain

UQ with UQLab Community Q&A and How To
,
1

Hi, UQLab!
I have some question about variable domain.
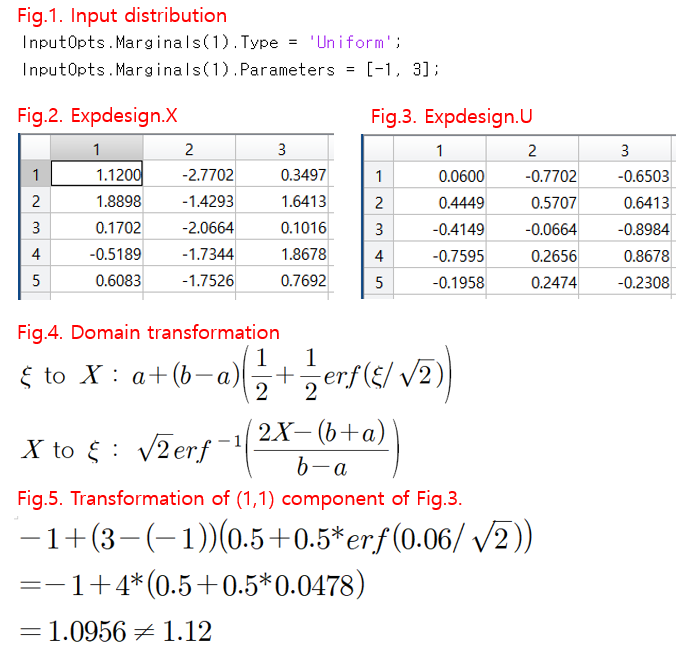
image
I created a Date driven PCE model, of which x1 was set as shown in Fig.1.
Because it was assumed to be a uniform distribution, the polynomial follows the Legendre polynomial, and the scale of the variable is rescaled from [-1, 3] to [-1, 1].

In this case, Fig.4. According to the equations of Fig.2. and Fig.3.
I also confirmed that the variables were converted.

However, when the variable was directly converted using the equation in Fig. 4, the value was slightly different. (Fig.5.)

Is the expression I used wrong? why the value is different?

2

Hi @Chemicaleng,

I am not sure why, but your transformation seems to involve a normal distribution.

I think the correct transformation here is from a uniformly distributed variable ([-1, 3]) to another uniformly distributed variable of different bounds ([-1, 1]). It should be (using your notation):

\xi \rightarrow X: \frac{b-a}{2} (\xi + 1) + a
X \rightarrow \xi: \frac{2}{b-a} (X - a) - 1

Plugging in \xi = 0.06 should give you 1.12.

I hope this answers your question.

3

Thank you very very much :slight_smile:
Best regards