Sensitivity analysis from simulation data

UQ with UQLab Community Q&A and How To
1

Hello, I have 3 input parameters: X1, X2, and X3 that I ran through a CFD model 50 times to obtain Y1, which is my output. So I’m trying to perform sensitivity analysis to get the sensitivity indices.

I used PCE to construct a surrogate model so I can perform the sensitivity analysis and this is the code:

X = load(‘X.csv’);

Y = load(‘Y.csv’);

% Define input parameters

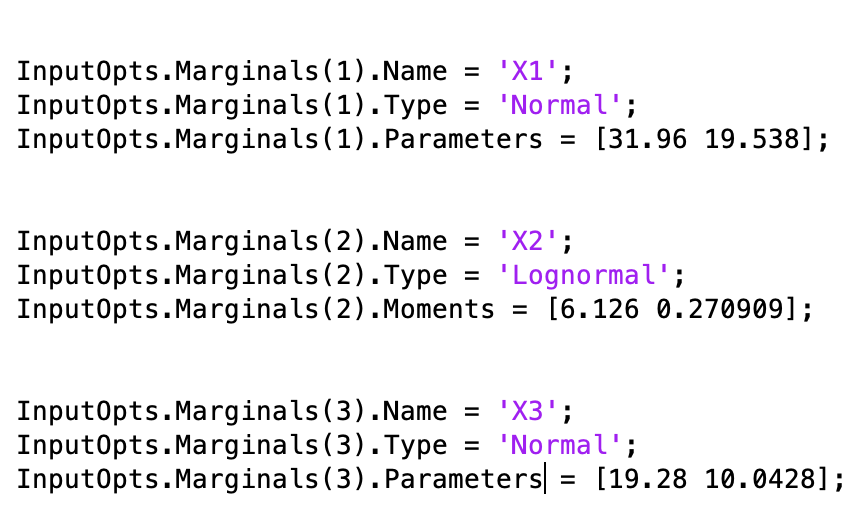
InputOpts.Marginals(1).Name = ‘X1’;

InputOpts.Marginals(1).Type = ‘Weibull’;

InputOpts.Marginals(1).Moments = [36.2 1.14642];

InputOpts.Marginals(2).Name = ‘X2’;

InputOpts.Marginals(2).Type = ‘Weibull’;

InputOpts.Marginals(2).Moments = [6.16 0.118322];

InputOpts.Marginals(3).Name = ‘X3’;

InputOpts.Marginals(3).Type = ‘Weibull’;

InputOpts.Marginals(3).Moments = [35.8 1.14642];

myInput = uq_createInput(InputOpts);

%Select PCE as the metamodeling tool

MetaOpts.Type = ‘Metamodel’;

MetaOpts.MetaType = ‘PCE’;

% Use input parameters

MetaOpts.ExpDesign.X = X
MetaOpts.ExpDesign.Y = Y

% Set the maximum polynomial degree to 5

MetaOpts.Degree = 1:5;

% Create the metamodel object and add it to UQLab

myPCE = uq_createModel(MetaOpts);

% Print a summary of the resulting PCE metamodel

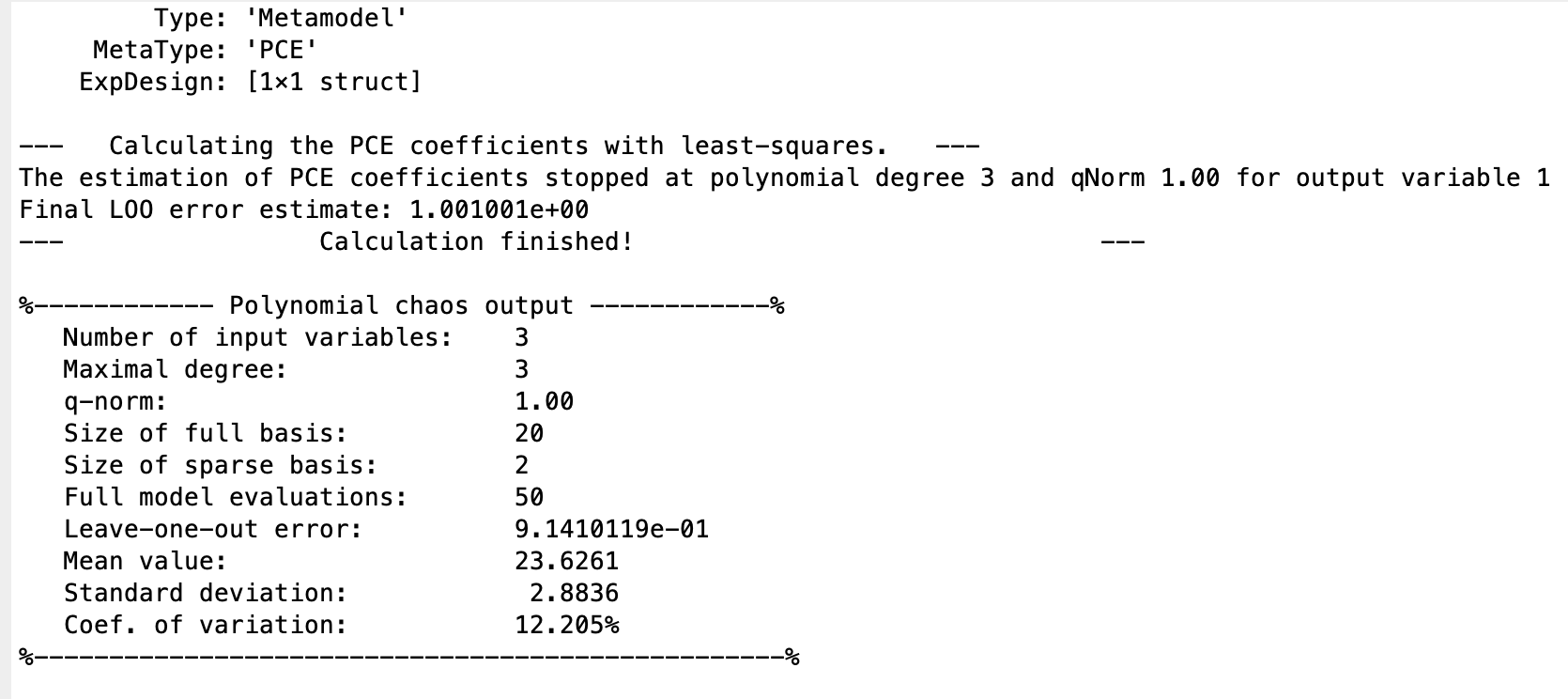
uq_print(myPCE);

% Computing Sobol indices

SobolOpts.Type = ‘Sensitivity’;

SobolOpts.Method = ‘Sobol’;

SobolOpts.Sobol.Order = 1;

mySobol = uq_createAnalysis(SobolOpts);

% print the Sobol’ indices
uq_print(mySobol)

% display the Sobol’ indices
uq_display(mySobol)

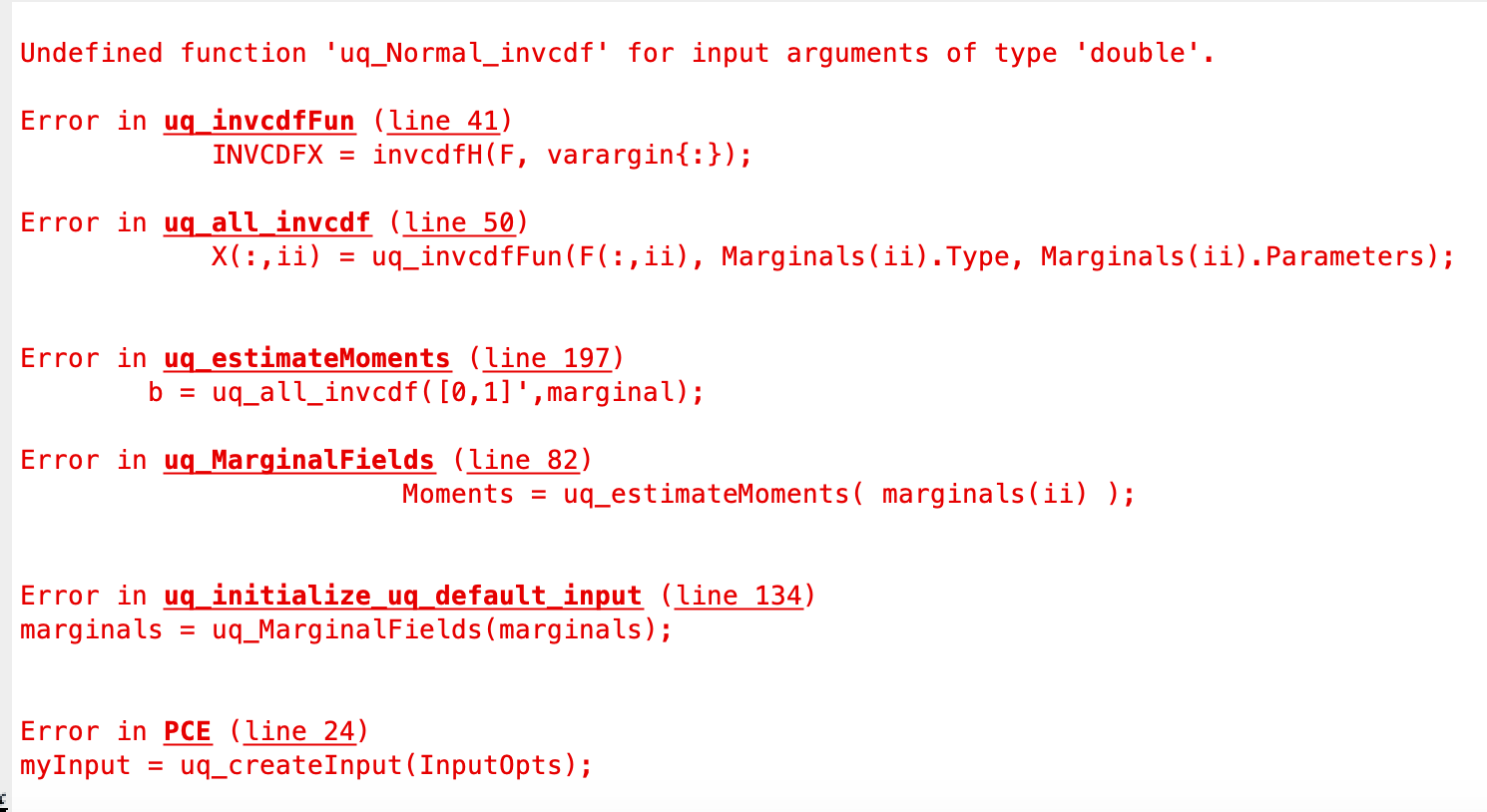
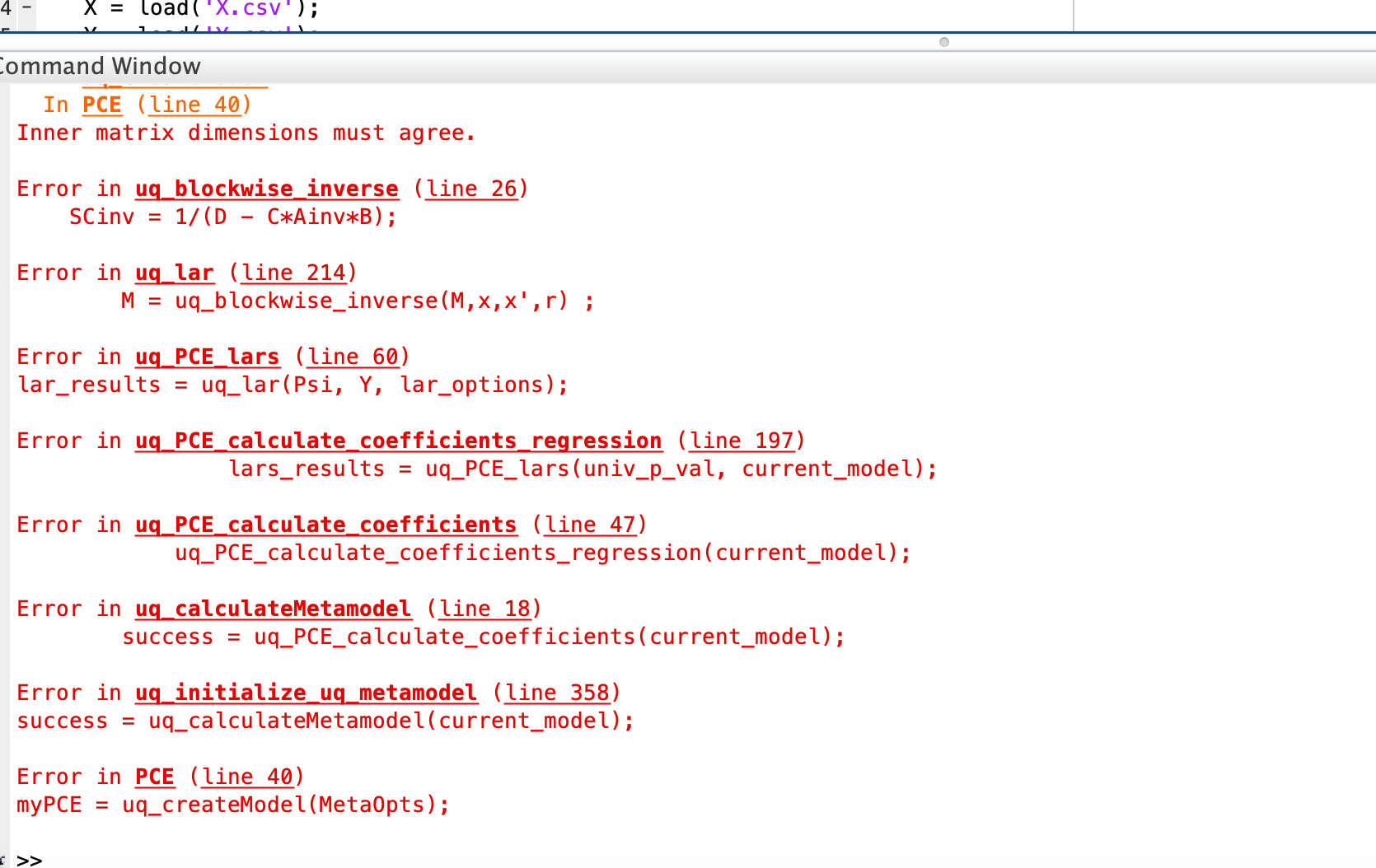
The first and second sobol indices were both 1, so I’m wondering where I went wrong. I’ve attached the data as well.
parameters.xlsx.zip (28.8 KB)

3

Hi @LorenzoVonMT ,

Before analyzing what might have gone wrong with the Sobol’ sensitivity analysis,
it might be a good idea looking at the previous steps, namely the INPUT and the PCE (did you check how good the resulting PCE model is before carrying out the sensitivity analysis? You can check its LOO error, for instance).

For instance, if I plot both your input data and the INPUT object, it seems the data does not correspond to the Weibull distribution specified in the INPUT object.

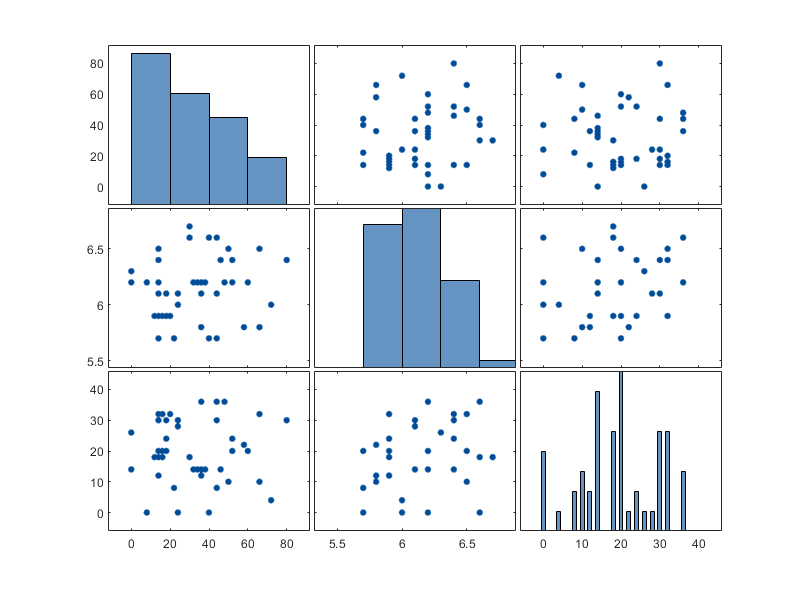Figure 1: Scatter plot matrix of the data (X). 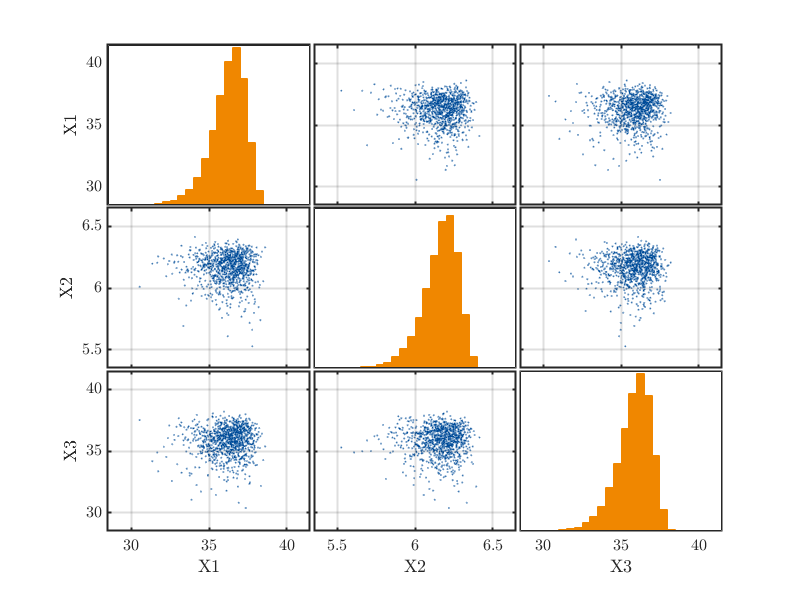Figure 2: Scatter plot matrix of the Weibull distributions specified in the INPUT object.

Also, did you round the values of the generated sample off? While rounding off the sample values might not affect your CFD simulation, I think they will affect the PCE computation.

Could you perhaps double check if you have generated your input (column 1 to 3 of the attached Excel sheet) from the proper marginal distribution? Also, make sure if you have specified the Weibull distribution correctly (moments vs. parameters is one typical source of problems).

I hope this helps!

PS: If you use the new inference capability of the UQLab INPUT module, the module will indeed fail to fit a Weibull distribution to it.

InputOpts.Inference.Data = X;
myInput = uq_createInput(InputOpts);
1 Like
4

Thanks for the reply @damarginal. When I used the distributions with the highest P values, I get the following errors:
Screen Shot 2020-09-17 at 12.53.38 PM
Screen Shot 2020-09-17 at 12.56.15 PM
Which is why I used the weibull distribution. Which distribution would you recommend for this dataset?

Also, this is the output of the PCE. The LOO error was quite large
Screen Shot 2020-09-17 at 12.59.22 PM
I also didn’t round the values of the output.

5

With such a high LOO error, I guess, you should be careful moving forward using the PCE metamodel for anything, including sensitivity analysis.

I previously assumed that X was generated using UQLab or, at least, that you know their origin. So maybe I should have asked you earlier, how did you get the values of X?

I also asked whether you somehow rounded off the inputs (X) because by looking at the inputs, especially X1 and X3, they are all integers and these are not typically sample values from a continuous distribution.

Now if you actually don’t know the underlying distribution of X, then you can use the inference capability of UQLab. UQLab will then try to fit various distribution families on the data and give you the best one (based on some statistical criteria). The minimum working syntax is the one I posted above in the PS. For details, you might want to check the relevant UQLab examples out such as Input Module: Inference of Marginals as well as the Statistical Inference User Manual.

So instead of specifying the marginals manually, you can then use the resulting INPUT object to create a PCE metamodel like you did before.

6

The values of X represent location coordinates of a tube in the CFD model, X1 ranges from 0 to 80 degrees, X2 ranges from 5.7 to 6.7 cm and X3 ranges from 0 to 40 degrees. An optimization scheme optimizes these 3 input parameters to achieve a target value which is my Y matrix. So those values were generated by the optimization scheme within the ranges above.

I used inference capability and this is the output
Screen Shot 2020-09-17 at 10.23.57 PM
However, I got this error when I ran the PCE
Screen Shot 2020-09-17 at 10.21.35 PM

Would you say I should give up using PCE or is there a better way to perform this sensitivity analysis?PCE.m (1.2 KB)

7

I think, there are a couple of interesting things to note here:

  1. I’m not sure why, but don’t you find it’s rather strange that the fitted marginal for the first input variable (X1) has the mean and standard deviation that are completely off from the data? They are off by one order magnitude away (the mean and standard deviation of X1 from the Excel sheet is 31.96 and 19.5938, respectively). The other two look reasonable. It would be interesting to know what’s the issue here (UQLab? Misspecification somewhere?).
  2. Because the original X came from some optimization scheme, I think we should proceed carefully. We might get a PCE model eventually but then it would only be valid for the space covered by (I think) biased input data.
    If we then move on to compute Sobol’ sensitivity indices then you should also take this into consideration. The results (and interpretation) of the Sobol’ sensitivity analysis depends on the distribution of the input. With inference, you can get fitted marginals for the input, but because the data is coming from an optimization scheme (so it may be biased, not random, or does not cover the actual space of interest), the fitted marginal may not represent the actual input correctly. I guess, in the end, it would depend on the purpose of the sensitivity analysis. Are you looking for the most important variable of the model itself or in the optimization process of the model, or maybe something else?
8

Yes, I found it odd so I used the correct mean and standard deviation values for X1. I also forgot to mention it in my previous reply but I moved the location of the tube in the CFD model and generated a new set of input parameters. I did this so that the input parameters would not have any zero values in order to fit more distributions. I have attached an excel sheet of the new input parameters.

I see your concerns about using PCE on this dataset, what I want from this sensitivity analysis is to get the contribution of each parameter (X1,X2,X3) to the output (Y1).
X.csv.zip (820 Bytes)

9

How expensive is running the 50 CFD simulations? If it’s still feasible maybe you can generate new runs, this time with the appropriate marginals and an LHS sample with which you can have more general results (considering you want the actual contribution of parameter on the model, and not the optimized model). If there’s no specified marginals, uniform distribution can be used for preliminary study.

10

It’s quite expensive, it runs at 3 simulations per day so it takes about 2 weeks. Would it make sense to multiply the input parameters by a certain factor in order to obtain the appropriate marginals?

11

@damarginal
I have talked to my advisor and he said it’s fine to transform the input parameters (X1,X2,X3) by a certain factor in order to have the appropriate marginals to run the PCE analysis. What do you think about this?

12

Hi @LorenzoVonMT,

I’m not so sure about that…what kind of factor are we talking about here? How do you plan to compute it? and what do you mean by the appropriate marginals in this case? Perhaps, I’m simply not familiar with your proposed approach…:sweat_smile:

13

@damarginal So the problem I’m having is that the distribution of my input parameters (X1,X2,X3) is causing the PCE analysis to fail, so I was thinking maybe transforming them by a certain factor could help because the input parameters are just a set of coordinates, whether they’re in feet or meters doesn’t change my output Y, so transforming the input will not change my output either.