The Rosenbrock’s function, also known as the valey or banana function, is commonly used as a test function for optimization algorithms, particularly for gradient-based algorithms since convergence towards its optimum is rather challenging (Forrester et al., 2008; Picheny et al., 2012).
Description
The analytic expression of the Rosenbrock’s function is given as:
where \mathbf{x} = \{x_m,\}_{m=1}^{M} are input variables; and M is a positive integer.
Figure 1 and 2 show the surface and contour plots of the 2-dimensional Rosenbrock’s function evaluated at \mathbf{x} \in [-10, 10]^2.
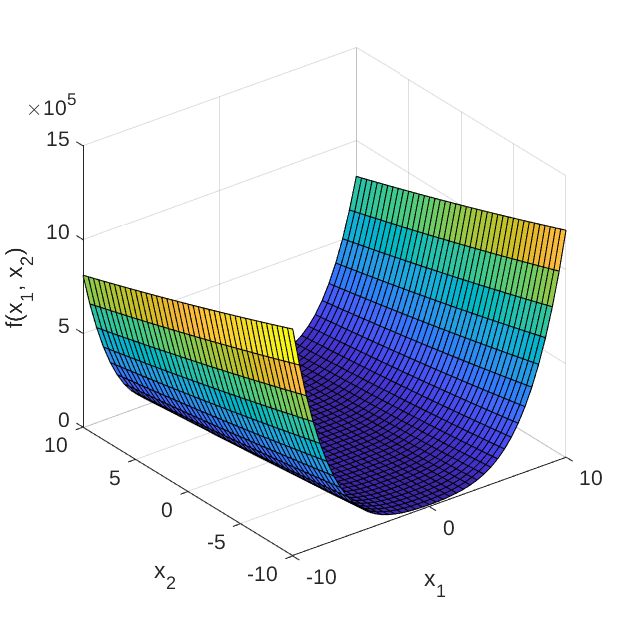
Figure 1: Surface plot of the 2-dimensional Rosenbrock’s function.
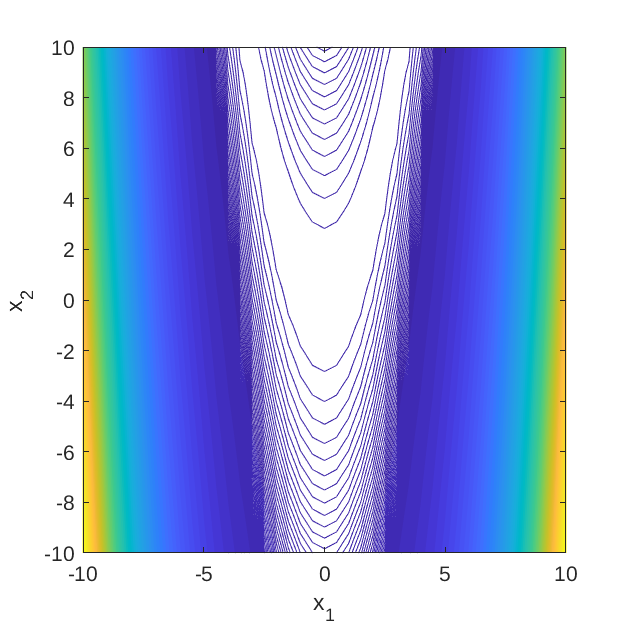
Figure 2: Contour plot of the 2-dimensional Rosenbrock’s function.
Inputs
The function is typically evaluated on the hypercube \mathbf{x} \in [-5, 10]^M. For computer experiment purposes, the input variables are modeled as independent uniform random variables.
| No | Variable | Distribution | Parameters |
|---|---|---|---|
| 1 | x_1 | Uniform |
x_{1,\min} = -5, x_{1,\max} = 10 |
| \vdots | \vdots | \vdots | \vdots |
| M | x_M | Uniform |
x_{M,\min} = -5, x_{M,\max} = 10 |
Reference values
The Rosenbrock’s function is a unimodal function and its global minimum, f(\mathbf{x}^*) = 0 is located at \mathbf{x}^* = (1, \ldots, 1).
Resources
The vectorized implementation of the M-dimensional Rosenbrock’s function in MATLAB as well as the script file with the model and probabilistic inputs definitions for the function in UQLAB can be downloaded below:
uq_rosenbrock.zip (2.2 KB)
The contents of the file are:
| Filename | Description |
|---|---|
uq_rosenbrock.m |
vectorized implementation of the Rosenbrock’s function |
uq_Example_rosenbrock.m |
definitions for the model and probabilistic inputs in UQLab |
LICENSE |
license for the function (BSD 3-Clause) |
References
- A. Forrester, A. Sóbester, and A. Keane, Engineering Design via Surrogate Modelling: A Practical Guide, West Sussex: John Wiley & Sons Ltd., 2008, pp. 196-197. DOI:10.1002/9780470770801
- V. Picheny, T. Wagner, and D. Ginsbourger, “A benchmark of kriging-based infill criteria for noisy optimization,” HAL, hal-00658212, 2012. URL