Hi, UQLab 
First of all, really really thank you for your interesting software.
I am majoring in Chemical Engineering, and since most of the data in Chemical Engineering is strong or complex, it is very difficult to obtain a mathematical expression. Therefore, i want to optimize using only data. (Metamodeling techniques will use PCE)
source : Reliability-Based Design Optimization of a Large-Scale Truss Structure Using Polynomial Chaos Expansion Metamodel
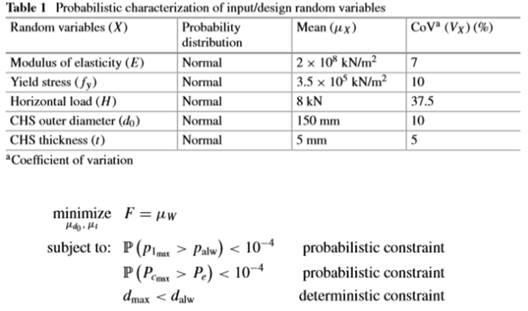
In the above study, they are optimizing in two stages. First, the underlying function is approximated by PCE metamodeling using 1200 data extracted through LHS. After that, select the optimization technique (GA, PSO …) to optimize. As you can see in the picture above, they are setting the probability of failure to 0.0001 to derive the result. As a result, considering three environmental uncertainties, the optimal solution is F = 27.88 when t = 4.5mm, d=165mm
In order to apply the above research to chemical engineering, i am learning RBDO, an example of UQLab. However, I understand that the RBDO example of UQLab does not only use data but seems to know the limit state function and cost function. In other words, the above example and UQLab’s RBDO seem to have different optimization mechanisms.
Is it possible to optimize only data(data driven not mathematical formula) using UQLab source? I want to use failure probability without setting limit state function or cost function.