Hello UQWorld!
I have the following question. I am conducting a global sensitivity analysis (Sobol using Monte Carlo sampling) and was wondering if it is possible to redefine the size of the sampling vector obtained by the uq_getSample function or, alternatively, set a constraint between two parameters involved in the sensitivity analysis without changing their probabilistic density functions?
The model it’s a simple equation that has two parameters:
![]()
Parameter (a) needs to be modeled by a log-normal distribution and parameter (b) by a Normal distribution.
In order to guarantee the convergence of the model, it is required that the values of the function f(x) must be between ]0, 2[ i.e. 0 < f(x) < 2. This should always be accomplished, otherwise the results may diverge.
For the performed analysis I can’t redefine the density functions of the parameters like it was explained in the forum Topic: Variable-dependent constrain on parameters, because both parameters have different type of probability density functions.
I’ve tried to solve this problem by eliminating sampling values that do not meet the given condition, as it’s shown below.
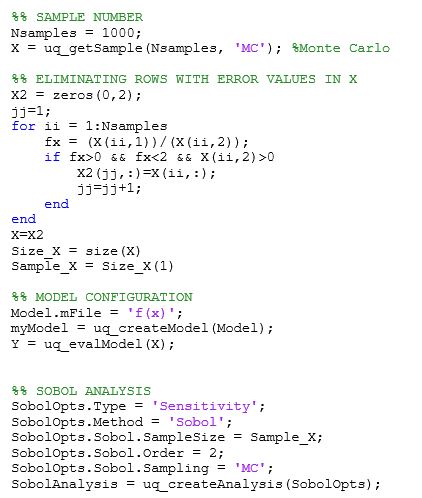
But this solution generates an error on dimension mismatch after running the Sobol’ analysis:

The model fails when it tries to calculate the total Sobol’ indices on the uq_sobol_indices core, because tsindex is a NaN vector. This occurs since the AllValues vector in the uq_sobol_indices core includes NaN values.
Since the uq_evalModel core does not show its code, it is assumed that the modified sample has not been evaluated, but rather the initial sampling.
Is there a way to evaluate a bounded sample or model the dependency between the parameters without changing the distribution functions?
I will be grateful for any recommendation,
Thanks,
Isabelle