PCE: can the output PDF be bounded?

UQ with UQLab Community Q&A and How To
,
1

Dear all UQ people

I have a “silly” question for you :upside_down_face:

I am building a PCE for 2 model outputs, namely H/S(t) and L/S(t), and they are computed in 7 time steps. The PCE is built using LARS method, and with the following characteristics:

  • number of simulation N_{sim}=7000
  • DegreeEarlyStop = false
  • metamodel.TruncOptions.qNorm = [0.9 0.95 0.975]
  • metamodel.Degree = 6:11;
  • Input dimension M=7

After the PCE finds the best qNorm, the best Degree, I get my 2 PCEs.
Successively, I create a new sample set, say N_{sample}=10000 samples, to evaluate the created PCE and check the validity of the surrogates. In other words, I want to check how accurately they approximate my model.

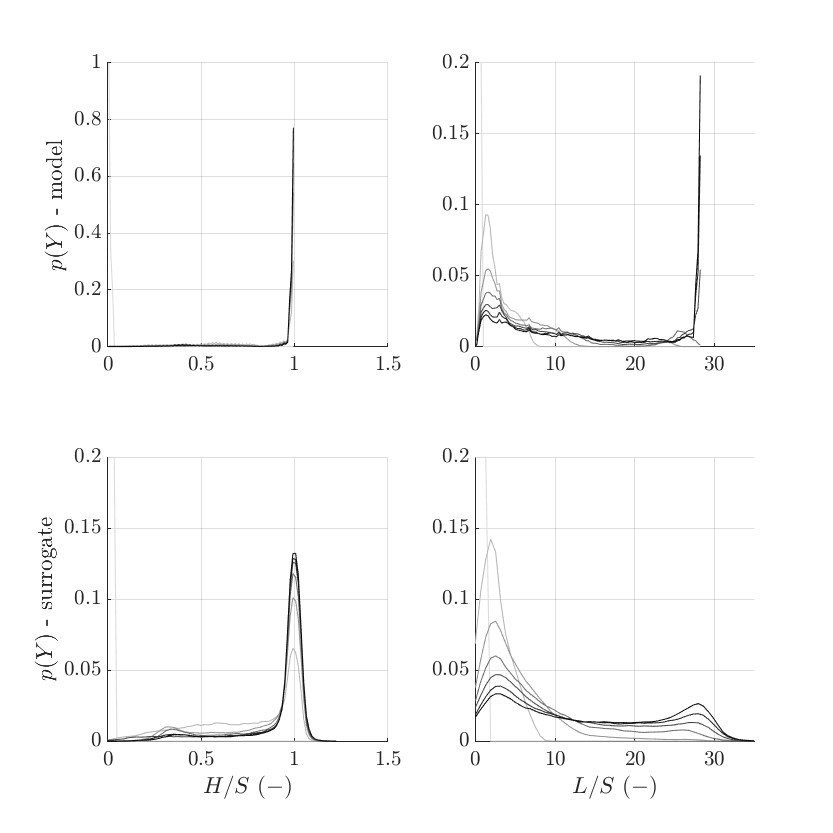
To check this, I evaluate the PCE, and plot the PDF functions of both the model’s outputs (H/S(t) and L/S(t)) and the surrogate’s outputs (\widehat{H/S}(t) and \widehat{L/S}(t)). You can see the results in the following picture. Model’s outputs are on the top row, and surrogate’s ones are on the bottom.

ModOut_SurrOut_prob

The PCEs errors (LOO, ModLOO, and NormEmpErrr) are reported here for outputs H/S before and L/S after.

% ::::::::: H/S :::::::::
LOO	                ModifiedLOO	        normEmpErr
0	                0	                0
0.0090583273425265	0.0129604505985762	0.00617285424918898
0.0224145486882809	0.0299271425113136	0.0159058780792346
0.0256757113910335	0.0352438072675073	0.0171982084514020
0.0218081098264392	0.0303681327153788	0.0145129841068436
0.0364352216699990	0.0514145886913357	0.0234572158255180
0.0446097448909121	0.0602193012041774	0.0296089961441069

% ::::::::: L/S :::::::::
LOO	                ModifiedLOO	        normEmpErr
0	                0	                0
0.0226401481139822	0.0288834103586079	0.0175835159153482
0.0520955801100249	0.0686993448933377	0.0385835562524133
0.0526829843782030	0.0648190913371306	0.0425621568554726
0.0555146490807771	0.0695122989997526	0.0451366872767112
0.0565982366525505	0.0673343001096283	0.0476579480569029
0.0488834208272997	0.0618057542342229	0.0389684913850232

As you may notice, the model’s outputs are bounded to the upper limits H/S=1 and L/S=26. However, the PCE is not able to model these bounded results.

I know that by nature, the PCE has a hard time modeling this particular behavior due to the nature of the Askey basis polynomials. However, I wonder if there is a way to “adjust” this somehow. Considering the model output H/S, for example, there is no physical meaning for H/S>1. However, the PCE evaluates this because there is no imposed bound on some basis polynomial.

Do you have any idea how I can treat this?

Thank you in advance and all the best
Gianni

1 Like