Hi,
I am looking into Kriging metamodelling especially this example provided by UQLab below:
KRIGING METAMODELING: BRANIN-HOO FUNCTION
Is it possible to run a model with 5 probabilistic input models instead of only 1 or 2? I have an issue as how to obtain the figures displayed using the examples. The error message appears to be only 1 and 2 dimensional X’s are supported. Is it possible to make the figures for more than 2 inputs?
Thank you!
Visha
Hi @Vishashalu,
While it is always possible to evaluate a model with more inputs (if the model allows for it), UQLab only supports plotting the results of metamodeling up to 2 dimension.
Perhaps you can be more specific on what kind of plots you’d like to see for more than 2 input variables? If you, say make a sketch, what would be displayed?
Hi Damar,
Actually it is about the estimation of moments using these metamodels. Because I saw in the example under Kriging for the multiple input dimension topic, the Kriging predictor mean and variance can be quickly visualized using the uq_display function.
So once we create the metamodel using Kriging and PCE-Kriging methods and with my 5 input model, I am unsure of how to obtain these statistical moments similar to PCE model for e.g. with the subtopic example on the ( PCE METAMODELING: ESTIMATION OF STATISTICAL MOMENTS MONTE-CARLO- VS PCE-BASED ESTIMATION OF MOMENTS)
I just wanted to know how can I see what the comparison of MCS based model and the metamodels based moments looks like.
Thanks!
Best regards,
Visha
For PCE metamodels, the first and second moment can be directly obtain from the coefficients, as you seen in the example you mentioned. However, for Kriging and PC-Kriging, you basically need to do Monte Carlo simulation but by using the metamodel instead of the full computational model. That is: generate (input) sample points, evaluate the metamodel, and then compute the mean and standard deviation (or variance) from the outputs.
Assuming you have created a Kriging metamodel stored in myKriging, then:
% Get a sample from the probabilistic input model
X_ED = uq_getSample(1e4,'LHS');
% Evaluate the metamodel on the current experimental design
Y_Krg = uq_evalModel(myKriging,X_ED);
% Calculate the moments
mean_Krg = mean(Y_Krg);
std_Krg = std(Y_Krg, 0, 1);
Note that the sample size to estimate the moments can be much larger (say, \sim 10^4) than the sample size to create the metamodel (say \sim 10^2). You can also plot the histogram of the metamodel prediction to see how the values distributed.
In the example PCE METAMODELING: ESTIMATION OF STATISTICAL MOMENTS, the moments are directly taken from the coefficients of the PCE metamodels created by increasing sample sizes.
In that example, the convergence plot that comes after is custom made (i.e., not via uq_display), you can create the same for Kriging or PCK by replacing relevant code sections with the above procedure.
I hope this helps!
Hi Damar,
This answers my questions. Thank you so much for your inputs!
Because in my mind the metamodel helps to not burden computational cost for computing the statistical moments such as PCE which can be directly computed. So based on what you are saying here the Kriging and PCE kriging are not like that. It is because I have an issue with vectorizing my complex model, I do not where it went wrong, so having to evaluate the model for large sample size is going to be a huge computational cost. I will have to check again.
Thank you very much for your help!
Best regards,
Visha
Yes, PCE metamodels do have nice properties regarding moment estimation (among other things). However, once you have a Kriging or PC-Kriging metamodel the computational cost to compute a large number of sample points from the metamodel should be minor compared to running the full computational model (assuming your complex model is non-trivial to run). Furthermore, I think the evaluation of all metamodels in UQLab is vectorized.
Dear Visha
As Damar said, UQLab evaluates the metamodel in a vectorized way. However, there may be rare cases where the best way to evaluate the metamodel is not obvious. For example, see this post:
If you explain you computational model in more detail, I can hopefully say more about that.
Best regards
Styfen
Hi all
I am Roberto from University of Trento. I am new to UQworld.
Regarding this discussion, the BraninHoo function provides the nice plots of mean and variance of the Gaussian process, that I’m attaching. The dimension of the input here is 2 so clearly such plot representation is possible, but it wouldn’t be for higher dimensions.
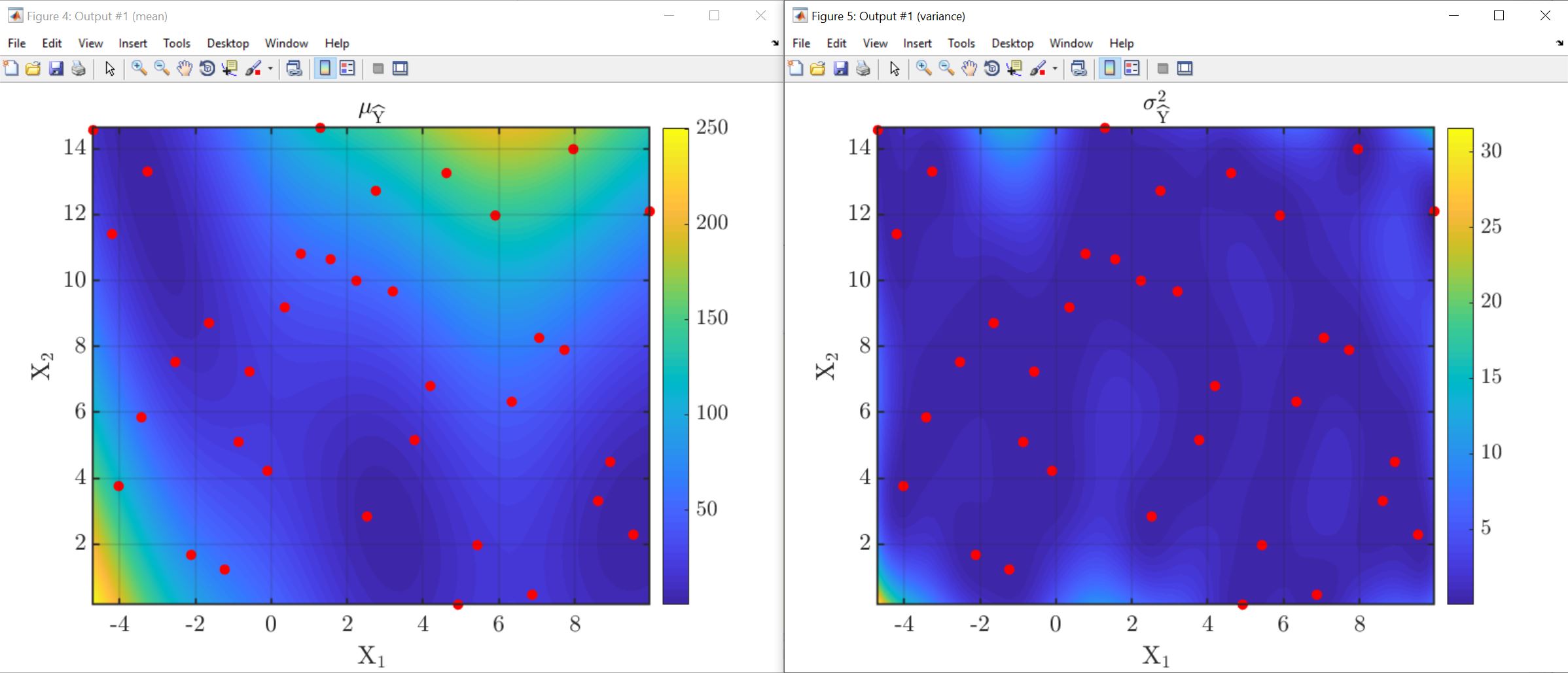
My question is how to obtain the same information for dimension of the input higher than 2 (e.g. my case is with 3)?
Thank you in advance
Roberto
Dear Roberto
You can obtain the mean and variance of your Kriging model at any point x as follows:
[Ymu,Yvar] = uq_evalModel(x)
Best regards
Styfen
Dear Styfen
Thank you so much. That’s what I needed.
Roberto
Hi Damar,
Yes indeed when I ran the metamodel to obtain the statistical moments, I got the solutions quite quick. I am wondering about the convergence plot you mentioned. Can you show me how you can implement it for Kriging for e.g. once you have found the metamodel. I tried following the methods from PCE METAMODELING: ESTIMATION OF STATISTICAL MOMENTS, however it did not work.
Thank you for your help!
Visha
Hi styfen,
My computational model is using orthogonal collocation method to solve boundary conditions problem where I need to choose no. of colloc points and fsolve to solve system of nonlinear equations to get the output. I failed to vectorized the inputs for the simple model (few uncertain inputs) and bit more complex model where it has more uncertain inputs. I did exactly following the examples shown to vectorized the inputs and I am not what went wrong.
Perhaps I can share you the error message here. It is definitely MATLAB problem not the UQLab I am sure.
Best regards,
Visha
Dear Visha
Regarding your first problem: The example you linked is for PCE. For PCE, you can derive the mean and variance analytically from the coefficients. For Kriging, this is not possible. You would need to evaluate your model on a fairly large number of points to get the global mean and variance. Essentially, you are performing an MC analysis on your surrogate. Note that I write “global” because this is not to be confused with the mean and variance that Roberto asked about.
As for your second problem, can you either provide us with your error message or, if possible, your code so that we can reproduce the error.
Best regards
Styfen
Hi Styfen,
Yes I understood from Damar’s explanation regarding obtaining the statistical moments from the Kriging method. I ran MC analysis on the surrogate with 10e3 samples and I got the global mean and variance pretty quickly. I hope I did it correctly though 
Damar further explained that the convergence plot that comes after showed for the PCE metamodel following the link example can be created for Kriging or PCK by replacing relevant code sections. So I wanted to find the similar convergence plot for Kriging first but not successful. Hence the confusion.
As for my 2nd issue, I will provide you the error message once I am done as soon.
Best regards,
Visha
Hi again,
Thanks for your help by the way and taking your time!
Visha
Hi Styfen,
I ran the complex model that I was talking about, it was really slow to run even with PCE metamodel method with sample design of 200. Once completed, I received the following error message:
Incorrect dimensions for matrix multiplication. Check that the number of columns
in the first matrix matches the number of rows in the second matrix. To perform
elementwise multiplication, use '.’.
Error in uq_lar (line 231)
cj = Psi’(Y - mu);
Error in uq_PCE_lars (line 64)
lar_results = uq_lar(Psi, Y, lar_options);
Error in uq_PCE_calculate_coefficients_regression (line 197)
lars_results = uq_PCE_lars(univ_p_val, current_model);
Error in uq_PCE_calculate_coefficients (line 47)
uq_PCE_calculate_coefficients_regression(current_model);
Error in uq_calculateMetamodel (line 18)
success = uq_PCE_calculate_coefficients(current_model);
Error in uq_initialize_uq_metamodel (line 362)
success = uq_calculateMetamodel(current_model);
I am not sure where is the problem to be exact.
Thanks,
Visha