Interpretation of posterior distributions

All About UQ UQ Discussion Forum
1

Hello,

I have set a Bayesian inversion, with a multiple output model, but the posterior distributions of my inputs raise questions. I am not sure of the relevance of my results.
Here is a description of my analysis:

  1. I have two inputs, E and c, which follow lognormal distributions.
  2. My model comes from a finite element software (ZSoil), with two outputs. It is surrogated with a PCK metamodel (Eloo ~ 10^-6 for both outputs).

I use the following code to create my inputs :

InputDist.Marginals(1).Name = ‘E’;
InputDist.Marginals(1).Type = ‘Lognormal’;
InputDist.Marginals(1).Moments = [8000 2000];
InputDist.Marginals(2).Name = ‘c’;
InputDist.Marginals(2).Type = ‘Lognormal’;
InputDist.Marginals(2).Moments = [10 ; 2];
myPriorDist = uq_createInput(InputDist);

To perform the inversion :

DiscrepancyOpts.Type = ‘Gaussian’;
DiscrepancyOpts.Parameters = 0.5 ;

myData.y = Observation (1,:);

Bayes.Type = ‘Inversion’;
Bayes.Data = myData;
Bayes.Prior = myPriorDist;
Bayes.ForwardModel = my_PCK;
Bayes.Discrepancy = DiscrepancyOpts ;
myBayes_stg3 = uq_createAnalysis(Bayes);

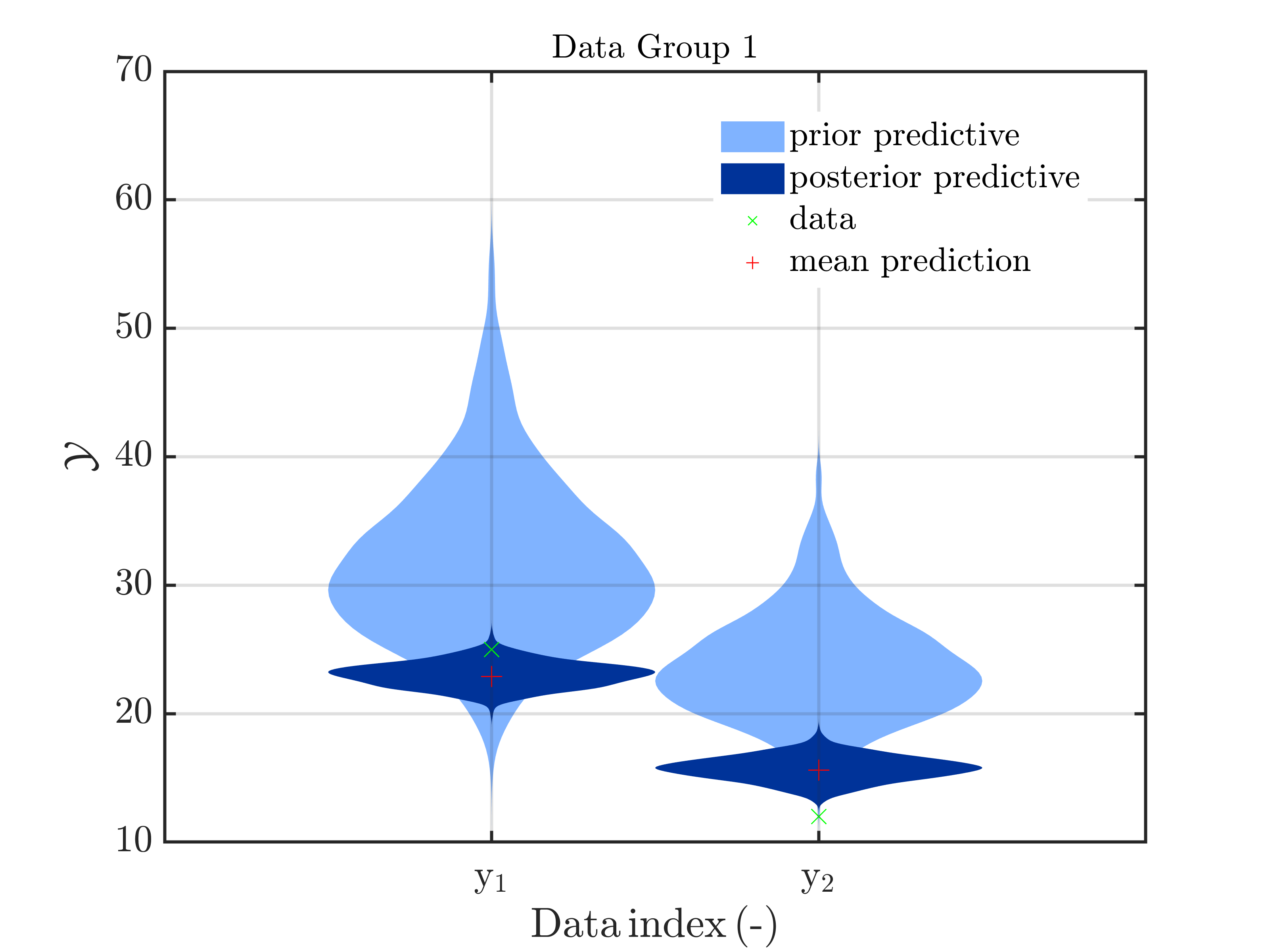
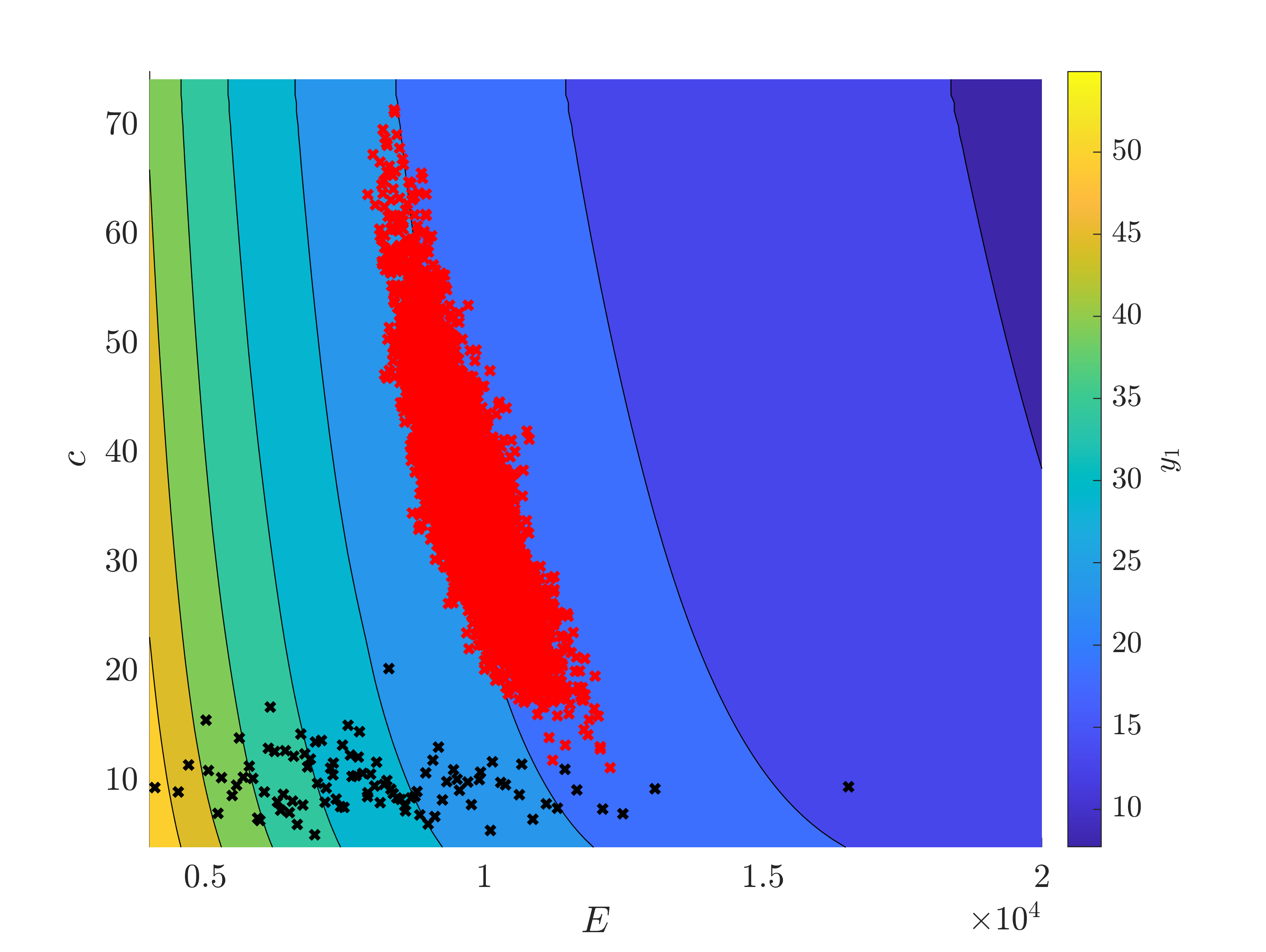
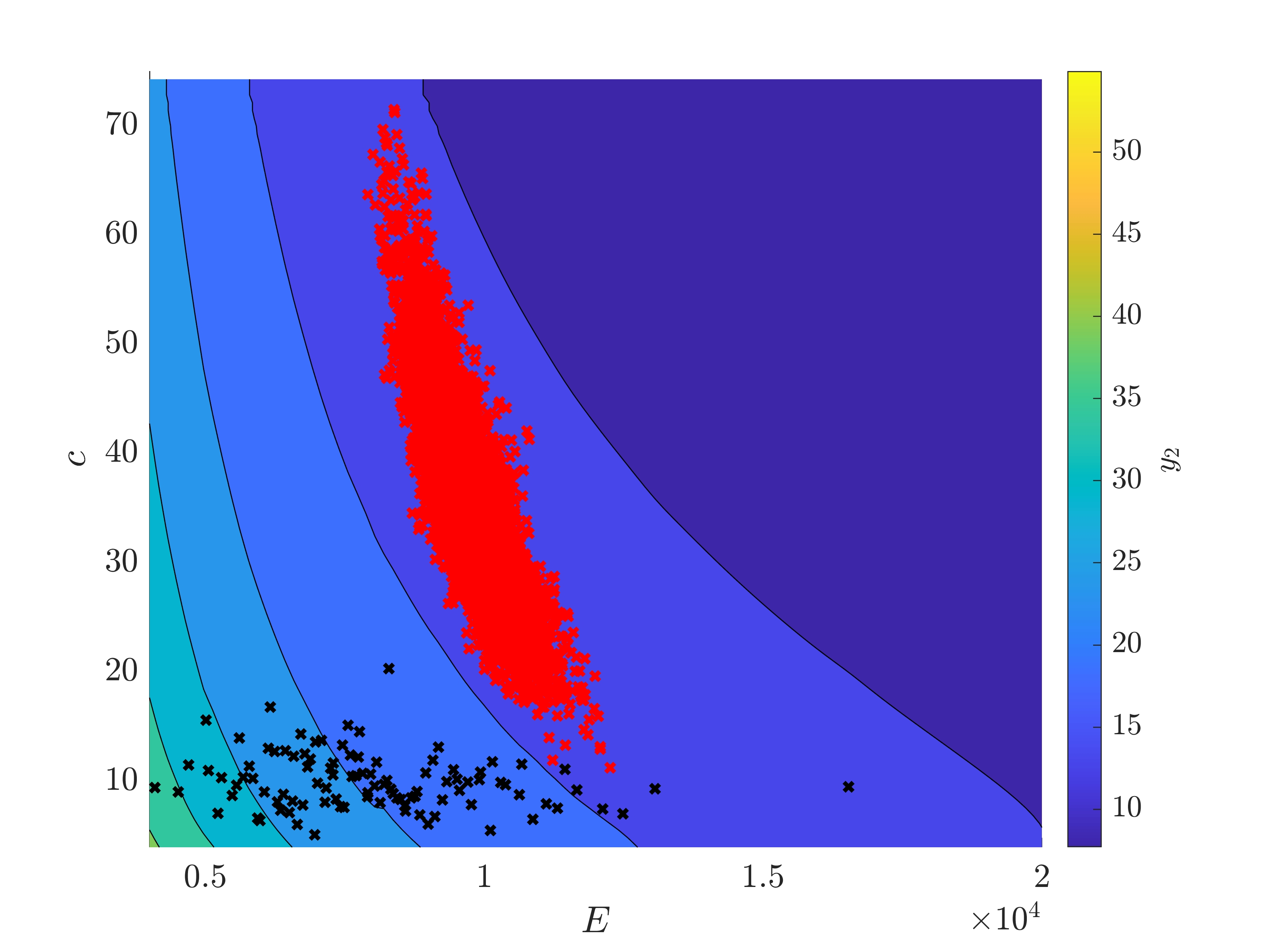
The measurement (25 ; 12) is quite far from the mean predicted value (30,22).

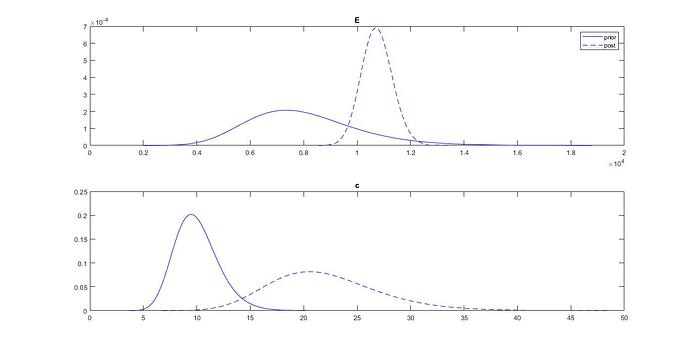
When I look at the prior and posterior distributions of my inputs, I have the following graph:

pdf_input
pdf_input1366×691 34.5 KB

My question is : is it possible, after a Bayesian inversion, that the standard deviation of an input increases ? On the graph, we can see that the standard deviation of c is higher after the inference. I thought, as the measurement brings information, that the standard deviation should be reduced.

I also have a technical remark : when I set the distribution of c to “constant”, in order to study only the influence of E on the inference, the Bayesian inversion should run without updating c, as shows the user manual. It seems in this case, the following error appears (before the beginning of AIES’s algorithm) :

Unrecognized property ‘Model’ for class ‘uq_model’.

Error in uq_initialize_uq_inversion (line 394)
ForwardModel(ii).Model = uq_createModel(ModelOpt,‘-private’);

Error in bayes_biais_uqlab (line 38)
myBayes_stg3 = uq_createAnalysis(Bayes_stage3);

It seems this message also appeared to @olaf.klein : is there something I can do to set c constant, without changing my model ?

Thanks a lot,

Marc Groslambert

2

Dear Marc Groslambert,

your problem is the same error if described in one of my posts in the topic
"Bayesian inference with multiple forward model with different numbers of provided measurements but with one common discrepancy model and parameter?

To be able to set c to constant you need to change the file
uq_initialize_uq_inversion.m of UQLab. The file can be found in the sub directory ./modules/uq_analysis/builtin/uq_inversion/ of your UQLab-Directory.
I suggest to start by creating a complete backup of all UQLab files in a new directory that is no sub-directory of your current UQLab-Directory. This allows to check latter, if an error is occurs due your changes of UQLab or if its is
already in the original UQLab-files.
As next step, change to the sub directory ./modules/uq_analysis/builtin/uq_inversion/ of your UQLab-Directory and create a copy of the file uq_initialize_uq_inversion.m denoted by uq_initialize_uq_inversion-org.m (do not use _org but -org such that Matlab will ignore this Backup file.)
Open the file uq_initialize_uq_inversion.m and replace in the lines 89 and 90 (and only in these two lines) ForwardModel by ForwardModelFromOptValue without activating the global replacement option of matlab and check afterwards that ForwardModel in line 392 is unchanged.
After saving the file, your should be able to run the code and the error message above should no longer show up.

Hope that this helps.

Greetings
Olaf

3 Likes
3

Dear Olaf Klein,

I followed your instructions step by step, they are very clear and precise. It worked perfectly, I can now run the algorithm with c as a constant.

Thank you for the helpful reply,

Marc

4

Hi @M_Groslambert

As pointed out by @olaf.klein the issue you observed is a known bug that will be fixed in the next version of UQLab.

Regarding your results, they are indeed puzzling. Could you provide a minimal working example that includes your PCK surrogate model and the Bayesian inversion setup?

Note: You can save the surrogate model after constructing it with uq_saveSession('mySession')

5

Hi @paulremo,

You’ll find attached the Matlab file : uq_world_bayes.zip (13.3 KB)

I set the PCK on 100 samples, which are saved in “100pts.mat”. The inputs and the model are also in this file, they are thus comments in the main Matlab file (code_uqworld_bayes).
In this example, we can see that the standard deviation of the second input c increases after the inversion, which is my main concern.

I made further tests about the constant input, in a second time. I 'd like to report what could be a bug. Indeed, when I run A_PCK_MCS (AKMCS with a PCK metamodel), with 2 inputs, an error appears if the first input is set to constant. An example is given in the file “code_UQ_world_APCKMCS.m”.

Thanks for your quick reply.

6

Hi @M_Groslambert

We are currently investigating the possible bug you uncovered in the reliability module. In the meantime, I looked into your model and the behavior you observed with the wider posterior variance can actually be expected.

The information gain from the supplied data results in a reduction of the predictive variance as can be clearly seen from comparing the prior and posterior predictive distributions with

uq_postProcessInversion(myBayes, 'priorPredictive', 1e3)
uq_display(myBayes, 'predDist', true)

which results in the following plot
predDist

Unless the forward model is linear, this does not require a reduction in the posterior distribution’s variance. Your (surrogate) model’s nonlinearity can be easily seen from the PCK model response:

Y1 Y2

The red \times are the posterior sample and the black \times are the points used to construct your PCK surrogate model. The posterior results are surely not surprising considering that the supplied data are y_1=25 and y_2=12, which is precisely where the posterior points concentrate in the respective plots.

The fact that the posterior lies quite far away from the prior bulk means that you can probably not trust the PCK surrogate model to be accurate w.r.t. posterior predictions. There is a vast amount of literature that discusses adaptive surrogate modeling approaches that are designed specifically for these situations (e.g. https://doi.org/10.1137/130938189).

As a quick solution to your problem, I suggest you evaluate your original model at a sample of the posterior distribution, construct a surrogate model with those points, and redo the Bayesian computation.

Hope this helps and let me know how it goes.

I attach the plot functions here: plotBayesPCK.m (1.6 KB)

3 Likes
7

Thanks for reporting the bug! We (mainly @moustapha) looked into it and there is indeed an issue with using a PCK metamodel with constants in conjunction with AK-MCS. This bug will require some time to fix, but we will definitely address it in the next version of UQLab.

In the meantime, you can just avoid using constant variables by redefining your forward model (or writing a wrapper around it). Let me know if you need further help.

1 Like
8

Dear @paulremo,
The plot you provide are very relevant, and your interpretation is very helpful.

Thanks also for pointing out the difference in the support of the prior and posterior distribution. Doing a posterior PCK, as you suggest, could indeed be an efficient solution.

Also for this specific problem, maybe the issue comes from the inputs. A sensitivity analysis shows that c does not influence much the outputs, as it can be seen on your plot. I think a way to tackle this issue could be to set c constant, ie to redo the analysis with only one input, E.
Do you think it is consistent ?

Best regards

9

Dear @M_Groslambert

Sure, you could do another analysis assuming a constant value for c. But this assumption should be based on knowledge about the parameter c and not just because the analysis becomes more difficult with a full prior distribution.

If you can justify a constant value for c a priori, in my opinion, you are good to go.

1 Like
10

Hi @paulremo,
I understand what you mean, it is a precious piece of advice.
Thanks !