Input distribution and data driven PCE

UQ with UQLab Community Q&A and How To
, ,
1

Ask a question about copula.
‘uq_Example_input_02_MarginalsAndGaussianCopula’

I would like to ask a question based on the example above.

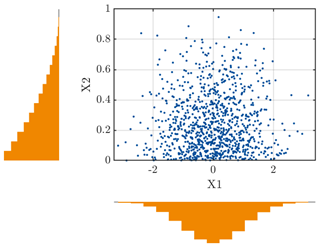
image

X1 is set to gaussian [0, 1] and X2 is set to beta [1 3].
Y = f (X1, X2)
In my opinion, I confirmed that the distributions of X1 and X2 are the gaussian and beta distributions respectively, and understood that they are the data points to extract the blue points.

  1. The data distribution is not known until the data is extracted. How do I set up? For example, do i has to make assumptions about uniform distributions, or inferred from the background knowledge of my data?

  2. What I want to do is data driven PCE.
    Y = f (X1, X2, X3, X4, X5)
    In the function configured as above, am i going to figure out the distribution of each of X1, X2, X3, X4, X5 by the method obtained in 1), and find the point of data to extract?
    (Like ‘uq_Example_Input_07_inferMarginalsAndCopula’ )

(I have a lack of understanding about copula, so I would like to ask a basic question.)

2

Hi

When setting up a UQ problem, you have to define what are your input distributions. Either by expert knowledge (e.g. selecting the distributions from the relevant literature), or to infer them from input data. In the latter case you should use the inference module of UQLab with your data to produce the proper INPUT object.
You may also refer to this post for more detailed information.

Best regards
Bruno