Input distribution and black box model

UQ with UQLab Community Q&A and How To
, ,
1

First of all, I would like to thank the people who developed wonderful software.

Chemical engineer believe that designing with uncertainty is essential because there is uncertainty in the input data, which affects the quality of the product.

Originally, neural nets were used to predict product performance. But I was fascinated by PCE’s ability to derive similar predictive performance with a small dataset.

What I want to do is use PCE as a predictor for the black box model.
So I am studying using uqlab example.

Examples\Metamodelling\PCE\uq_Example_PCE_05_TrussDataset.m

In the X data used in the example above, the third row(A1) has a minimum value of 0.001513 and a maximum value of 0.002611.
In the example code, the variable A1 is saved as shown below.

InputOpts.Marginals(3).Type = ‘Lognormal’
InputOpts.Marginals(3).Moments = [2.0e-3 2.0e-4]

  1. Can i know if the distribution is Lognormal by plotting the data? if the distribution of the data is not a known distribution like Lognormal or Gaussian, how do i enter the distribution?

  2. I think Moments should be entered considering the maximum and minimum values of the data.
    I am wondering why Moments is [2.0e-3 2.0e-4] in the above problem.

  3. [Additional question] Neural net trains the model with training data and evaluates the model with test data. In this example, do i think that the total of 10200 data is divided into 200 training data and 10000 test data? If yes, is there a ratio of dividing the number of data?

X 200 * 10 double, Y 200 * 1 double
Xval 10000 * 10 double, Y 10000 * 1 double

  1. [Additional question]
    The average of Y is -0.0794. If we assume that the system is reliable when Y is less than -0.1, can i determine the condition of the input variables at that time?

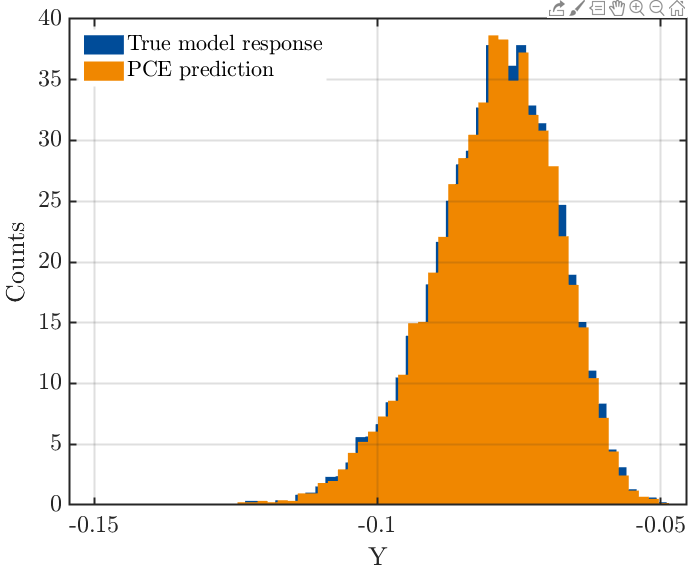
image

  1. [Additional question] Neural nets can create new functions that approximate underlying functions through weights and biases, and can be optimized through those functions. Is it possible to optimize using PCE like this?

  2. [Additional question] Is it possible to predict any single input data set using the PCE model?
    (pointwise prediction)
    [1, 2, 0,1 0.2]-> PCE Model-> [?]
    (4 dimension input)

2

Hi @Chemicaleng,

Thanks for your nice compliment to UQLab and welcome to UQWorld! :slight_smile:

Indeed, PCE perform quite well when compared to other machine learning methods such as neural networks or SVR (see e.g. Torre et al 2019, Timpe et al 2020). May I ask which publications you have read that inspired you to try PCE on your data?

Let me try to answer your many questions:

You can never be sure about the distribution of your data (unless you have generated it yourself from a known distribution). Choosing the input distribution is a modelling decision. You can decide based on looking at the histograms or plotmatrix, based on prior knowledge on bounds and moments, and/or based on physical reasoning. And/or you can use advanced mathematical techniques to select a distribution and parameters that fit the data best, which is easy with UQLab’s statistical inference module.

In the field InputOpts.Marginals(i).Moments you specify the mean, the standard deviation, and possibly higher order moments of the distribution (see e.g. section 2.1.1.2 of the input manual). The choice of these specific values for the moments of A1 is a modelling decision.

In this example, the training set (X,Y) contains 200 points, and the validation data set (Xval, Yval) contains 10000 points. The truss model is a toy problem, and it is cheap to generate a large validation set. We need the validation set here in order to demonstrate how the PCE performs on previously unseen data.
In real applications, it is typically very expensive to evaluate the model. Often, all available data points are used to train the model, and techniques like cross-validation are used to (hopefully) prevent overfitting.
In general, for PCE you handle the data exactly the same way as you would do for other machine learning techniques.

Can you clarify what you mean?

When you train a neural net, you are optimizing the weights and biases so that the data is approximated as well as possible (while preventing overfitting). When computing a PCE (using e.g. sparse regression), you determine the basis functions and coefficients so that the data is approximated as well as possible (while preventing overfitting). So if I understand your question correctly, the answer is yes, by definition.

Yes, the resulting PCE object is a uq_model which can be easily evaluated:

Xnew = [1,2,0.1,0.2];
Ynew = uq_evalModel(myPCE, Xnew)

It will be interesting to hear whether PCE are competitive with neural networks also in your application, let us know once you have the results! :slight_smile:

3

Thank you for your kind reply!
It is so helpful to me! :slight_smile: