How to determine the initial discrepancy parameter in the likelihood

UQ with UQLab Community Q&A and How To
1

Hello, all

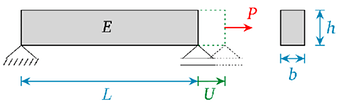
I am recently doing a Bayesian calibration of the classical elongation problem. The case is simple: We apply a force P on the beam, then we get a displacement u. All other variables (E,L,b,h) are constants.

image
image707×217 25.7 KB

The inversion principle works as:

Forward model: \mathcal{M}(p): U = \frac{PL}{Ebh}

The likelihood is constructed by the discrepancy between observation u and forward model \mathcal{M}(p)

\mathcal{L} (p,\sigma \mid u) = \frac{1}{(2\pi)^{{3}/2}\det(\boldsymbol{\Sigma}(\sigma))^{1/2}} \exp\left(-\frac{1}{2}\left(u - \mathcal{M}(p)\right)^{\mathsf{T}} \boldsymbol{\Sigma}(\sigma)^{-1}\left(u - \mathcal{M}(p)\right)\right)
\Sigma(\sigma) = \sigma^2 I

The discrepancy \sigma^2 is usually unknown, it is common practice for \sigma^2 inferred together with model parameter P. This requires the initial specification of a prior distribution of the distribution parameter \pi(\sigma^2), which UQlab document and examples adopt the mean of the observation.

Here come to my question: Since the discrepancy \sigma^2 is the error between the observation u and forward model \mathcal{M}(p), why should we take the mean of the observation as a prior for \pi(\sigma^2)? Personally I think it is too big. Why not take 1%-5% of mean of the observation as a prior for \pi(\sigma^2)?

The reason I propose this question is because when I doing the elongation beam problem. If I take mean of observation u as a prior for \pi(\sigma^2). The result looks like this (not good):
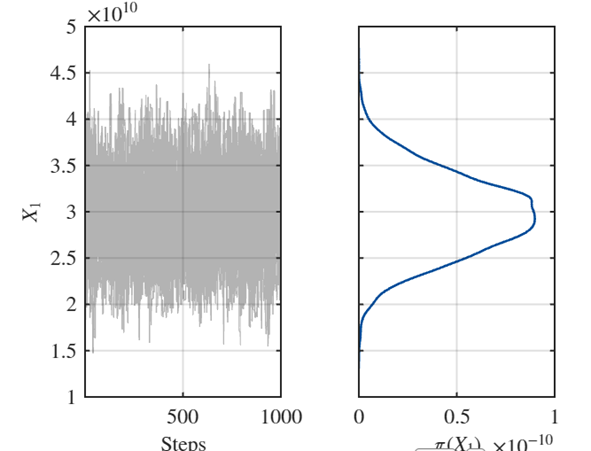
image

If I take 1% of mean of observation u as a prior for \pi(\sigma^2), the result looks like this (good):

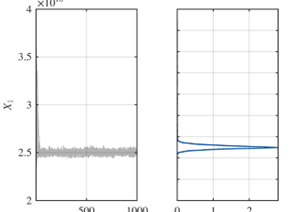
image

I understand the difference is from the setting of discrepancy \sigma^2, not from UQlab.

In summary: how can I determine a reasonable range for the discrepancy parameter \sigma^2? I understand that it must be related to the measurements u, but are there any rules for this? For instance, is 1%-5% of the measurement a reasonable range for a good prior for discrepancy? Because clearly, 1% of the measurement works perfectly for this elongation problem. But would this also apply to other, more general problems? I’m hoping to receive some guidance on this.

Any suggestions and comments will help

Best,
Ningxin

2

Dear @ny123

Thanks for your question about Bayesian calibration. In this process, the discrepancy term (modeled by zero-mean variance) can be interpreted in different ways:

  • if the model was perfect, and the discrepancy only corresponds to measurement error, it makes sense to use the supposedly known variance \sigma^2 of measurement error in the definition of the likelihood function.
  • In general we don’t have perfect models though, and part (often, the biggest part) of the discrepancy is due to this model error. In this case, it’s difficult to know a priori the variance of such model error term (already assuming that it is zero-mean is quite a strong hypothesis). That’s why we usually try to use a non informative prior on \sigma^2 in that case. The Jeffrey’s prior is a popular option:
\pi(\sigma^2) \propto \frac{1}{\sigma^2}

Yet UQLab cannot (currently) handle this prior. So in practice we use a uniform prior \pi(\sigma^2) \sim \mathcal{U}(0, UB) , where UB is a large value, yet commensurate to the magnitude of the observation data, so typically the square of the mean of the data (but you could also choose the empirical variance, maybe a multiple of it).

Back to the beam problem, if the data is informative for the calibration, then the choice of the prior distribution on \sigma^2 should not change so much the results. I hope this replies your question.

Best regards
Bruno

PS: in the case of discrepancy with unknown variance, the prior (e.g., the upper bound UB of the uniform distribution \sigma^2 \sim \mathcal{U}(0, UB)) should be for the variance \sigma^2, not for \sigma.
Don’t get confused with the values!

1 Like
3

Dear @bsudret ,

Thank you for your detailed explanation on Bayesian calibration discrepancy term. I appreciate the suggestion of using Jeffrey’s prior as another alternative option to uniform non-informative distribution for \sigma^2. I’ll dig more about Jeffrey’s prior this further as a potential solution.

And also, thanks UQlab for providing such a wonderful platform to receive help.

Best regards,
Ningxin