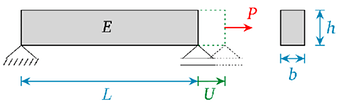
Hello, all
I am recently doing a Bayesian calibration with multiple forward models. Let us take an example of the classical beam problem. We have two forward models- \textbf{deflection model} (with two or more deflection outputs) and \textbf{elongation model} (with only one elongation output) as:
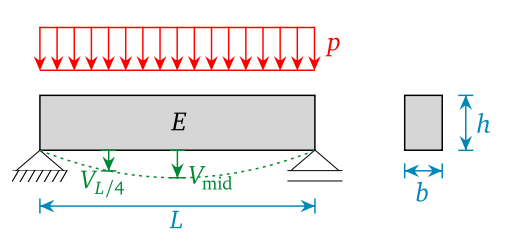
\textbf{Working principle for Bayesian inversion with multiple forward models:}
The basic principle for Bayesian inversion with multiple forward models is simply multiplying their likelihood (or sum their log likelihood). In custom loglikelihood, it is more like
log \mathcal{L_1} with deflection forward model \mathcal{M_1} is expressed as log \mathcal{L_1} (\boldsymbol{\vec\theta},\boldsymbol{\epsilon} \mid \boldsymbol{Y}) = \sum_{i}^{N}\left(-\frac{1}{2}\left(\boldsymbol{Y_i} - \mathcal{M_1}(\vec\theta)\right)^{\mathsf{T}} \boldsymbol{\Sigma}(\epsilon)^{-1}\left(\boldsymbol{Y_i} - \mathcal{M_1}(\vec\theta)\right)\right) - \frac{3N}{2}\log(2\pi) - \frac{N}{2}\log\left(\det(\boldsymbol{\Sigma}(\epsilon))\right)
log \mathcal{L_2} with deflection forward model \mathcal{M_2} is expressed as log \mathcal{L_2} (\boldsymbol{\vec\theta},\boldsymbol{\epsilon} \mid \boldsymbol{Y}) = \sum_{i}^{N}\left(-\frac{1}{2}\left(\boldsymbol{Y_i} - \mathcal{M_2}(\vec\theta)\right)^{\mathsf{T}} \boldsymbol{\Sigma}(\epsilon)^{-1}\left(\boldsymbol{Y_i} - \mathcal{M_2}(\vec\theta)\right)\right) - \frac{3N}{2}\log(2\pi) - \frac{N}{2}\log\left(\det(\boldsymbol{\Sigma}(\epsilon))\right)
So, the sum of the log likelihood space can be express as:
log \mathcal{L_{sum}} = log \mathcal{L_1} + log \mathcal{L_2}
\textbf{Problems encountered:}
The values of log \mathcal{L_1} and log \mathcal{L_2} are sometimes not comparable. For example, log \mathcal{L_{sum}} = (-100) + (-500). Apparently, we assume information from log \mathcal{L_1} and log \mathcal{L_2} are different. In this case, log \mathcal{L_1} plays a more important role for updating log \mathcal{L_{sum}}.
Is there any normalized way to consider log \mathcal{L_1} and log \mathcal{L_2} equally to update log \mathcal{L_{sum}} ? Any advice will be appreciated
Best,
Ningxin