The Gayton hat function is a two-dimensional limit state function used in Echard et al. (2013) as a test function for reliability analysis algorithms.
Description
The performance function is defined as:
where \mathbf{x} = \{U_1, U_2\} are standard normal random variables.
The failure event is defined as f(\mathbf{x}) \leq 0 and the failure probability P_f = \mathbb{P}[f(\mathbf{x}) \leq 0]. Figure 1 shows the scatter plot of 5\times 10^6 sample points, with each point categorized either as failed (f(\mathbf{x}) < 0) or safe (f(\mathbf{x}) > 0).
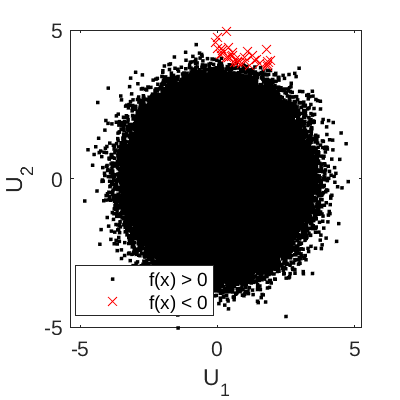
Figure 1: Scatter plot of 5 \times 10^6 sample points for the Gayton hat function.
Inputs
| No | Variable | Distribution | Parameters |
|---|---|---|---|
| 1 | U_1 | Gaussian |
\mu_{U_1} = 0, \sigma_{U_1} = 1 |
| 2 | U_2 | Gaussian |
\mu_{U_2} = 0, \sigma_{U_2} = 1 |
Reference values
Some reference values for the failure probability P_f from the literature are shown in the table below. Note that the values from Echard et al. (2013) are median values over 100 replications.
| Method | N | \hat{P_f} | \text{CoV}[\hat{P}_f] | Source |
|---|---|---|---|---|
| MCS | 5\times 10^7 | 2.85 \times 10^{-5} | 2.64\% | Echard et al. (2013) |
| FORM | 19 | 4.21 \times 10^{-5} | – | Echard et al. (2013) |
| IS | 19 + 10^{4} | 2.86 \times 10^{-5} | 2.39\% | Echard et al. (2013) |
| AK-IS | 19 + 7 | 2.86 \times 10^{-5} | 2.39\% | Echard et al. (2013) |
Resources
The vectorized implementation of the Gayton hat function in MATLAB as well as the script file with the model and probabilistic inputs definitions for the function in UQLAB can be downloaded below:
uq_gaytonHat.zip (2.2 KB)
The contents of the file are:
| Filename | Description |
|---|---|
uq_gaytonHat.m |
vectorized implementation of the Gayton hat function in MATLAB |
uq_Example_gaytonHat.m |
definitions for the model and probabilistic inputs in UQLab |
LICENSE |
license for the function (BSD 3-Clause) |
References
- B. Echard, N. Gayton, M. Lemaire, and N. Relun, “A combined Importance Sampling and Kriging reliability method for small failure probabilities with time-demanding numerical models”, Reliability Engineering and System Safety, vol. 111, pp. 232-240, 2013. DOI:10.1016/j.ress.2012.10.008.