Four-Branch Function

UQ with UQLab Benchmarks
, ,
1

The 2-dimensional four-branch function is a common benchmark problem in reliability analysis (Schueremans and van Gemert, 2005; Echard et al., 2011; Schöbi et al., 2017). The function describes the failure of a series system with four distinct limit state components.

Description

The mathematical formulation of the four-branch function reads:

f(\mathbf{x},p) = \min \begin{Bmatrix} 3 + 0.1(x_1 - x_2)^2 - \frac{x_1 + x_2}{\sqrt{2}}\\ 3 + 0.1(x_1 - x_2)^2 + \frac{x_1 + x_2}{\sqrt{2}}\\ (x_1 - x_2) + \frac{p}{\sqrt{2}}\\ (x_2 - x_1) + \frac{p}{\sqrt{2}} \end{Bmatrix}

where the input variables \mathbf{x} = \{x_1, x_2\} are modeled as two independent Gaussian random variables and p is a constant parameter. The default constant parameter value is 6.

The failure event is defined as f(\mathbf{x}) \leq 0 and the failure probability P_f = \mathbb{P}[f(\mathbf{x}) \leq 0]. Figure 1 and 2 show the surface and contour plot of the four-branch function, respectively. In Figure 2, the limit state function (f(\mathbf{x}) = 0) is shown.

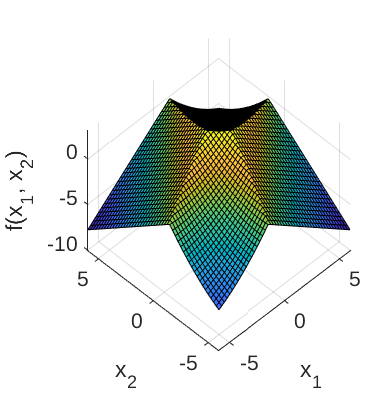
fourBranchSurface
Figure 1: Surface plot of the four-branch function.

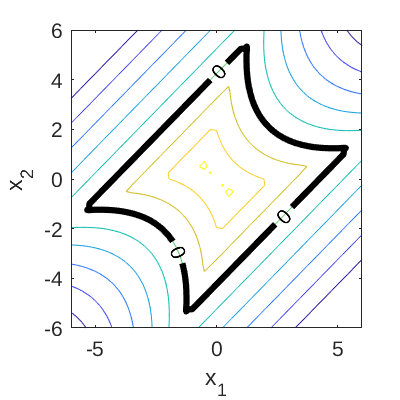
fourBranchContour
Figure 2: Contour plot of the four-branch function. The limit state function is also shown.

Inputs

The two input variables are modeled as independent Gaussian random variables.

No Variable Distribution Parameters
1 x_1 Gaussian \mu_{x_1} = 0
\sigma_{x_1} = 1
2 x_2 Gaussian \mu_{x_2} = 0
\sigma_{x_2} = 1

Constant parameter

The default value of the constant parameter p is 6.

Reference values

Some reference values for the failure probability P_f from the literature are shown in the table below.

Method N \hat{P}_f \text{COV}[\hat{P}_f] Source
MCS 10^8 4.460 \times 10^{-3} 1.5\% Schöbi et al. (2017)
MCS 10^6 4.416 \times 10^{-3} 0.15\% Echard et al. (2011)
IS 1469 4.9 \times 10^{-3} - Echard et al. (2011)

Resources

The vectorized implementation of the four-branch function in MATLAB as well as the script file with the model and probabilistic inputs definitions for the function in UQLAB can be downloaded below:

uq_fourBranch.zip (2.5 KB)

The contents of the file are:

Filename Description
uq_fourBranch.m vectorized implementation of the four-branch function
uq_Example_fourBranch.m definitions for the model and probabilistic inputs in UQLab
LICENSE license for the function (BSD 3-Clause)

References

  • B. Echard, N. Gayton, and M. Lemaire, “AK-MCS: An active learning reliability method combining Kriging and Monte Carlo simulation”, Reliability Engineering and System Safety, vol. 33, no. 2, pp. 145-154, 2011. DOI:10.1016/j.strusafe.2011.01.002
  • R. Schöbi, B. Sudret, and S. Marelli, “Rare event estimation using polynomial-chaos Kriging,” Journal of Risk Uncertainty in Engineering System, Part A: Civil Engineering, vol. 3, no. 2, 2017. DOI:10.1061/AJRUA6.0000870
  • L. Schueremans and D. van Gemert, “Benefit of splines and neural networks in simulation based structural reliability analysis,” Structural Safety, vol. 27, no. 3, 2005. DOI:10.1016/j.strusafe.2004.11.001