Exploring several solvers in Bayesian inversion based on explicit functions and 'black box models' (external datasets)

UQ with UQLab Community Q&A and How To
,
1

Hi, @paulremo
Recently, I perform Bayesian inversion comparison of several solvers (MCMC\SLE\SSLE) based on the sample given in uqlab uq_Example_Inversion_09_SamplingFree and uq_Example_Inversion_08_Surrogate combined with my own external dataset.

% my own external dataset
%% 2 - FORWARD MODEL
FILELOCATION = fullfile(uq_rootPath, 'Examples', 'SimpleDataSets',...
    'WDD_Experiment');
load(fullfile(FILELOCATION,'wdd_full_mode8_doe60.mat'), 'X', 'Y');
load(fullfile(FILELOCATION,'wdd_full_mode8_VAL30'), 'Xval', 'Yval');

%% 3 - INPUT MODEL
% Scaled prototype experimental dam
InputOpts.Marginals(1).Name = 'E1'; %Elastic modulus of the dam
InputOpts.Marginals(1).Type = 'Gaussian';
InputOpts.Marginals(1).Moments = [1.5e9 3e8]; % (Pa)

InputOpts.Marginals(2).Name = 'D1'; %The density of the dam
InputOpts.Marginals(2).Type = 'Gaussian';
InputOpts.Marginals(2).Moments = [2200 440]; % (kg/m3)

InputOpts.Marginals(3).Name = 'E2'; %Elastic modulus of the foundation
InputOpts.Marginals(3).Type = 'Gaussian';
InputOpts.Marginals(3).Moments = [3e10 6e9]; % (Pa)

InputOpts.Marginals(4).Name = 'D2'; %The density of the foundation
InputOpts.Marginals(4).Type = 'Gaussian';
InputOpts.Marginals(4).Moments = [2400 480]; % (kg/m3)

myInput = uq_createInput(InputOpts);

Then, Some interesting results were found：

  • For the given simply supported beam model in the above case, the results of the SLE solver are not satisfactory enough to achieve the purpose of parameter identification based on different NSamples; for the other two solvers, the posteriori values of input parameters tend to converge as the number of samples increases；

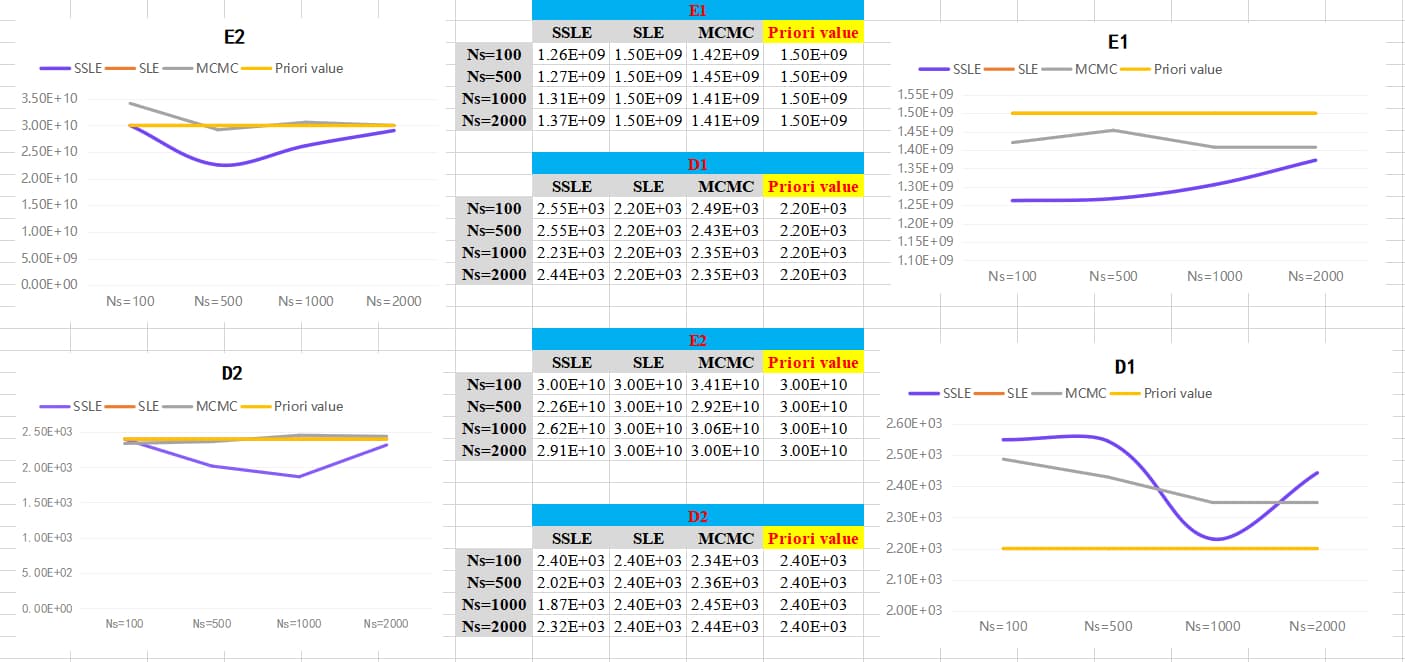
However, when I implemented the same operation using my own external dataset (black box model), I found a different result:

  • The SLE solver fails completely;
  • The MCMC and SSLE solvers, which have good applicability in the benchmark model with explicit functions, show unsatisfactory robustness here, Among them, the irregularity of the posterior value based on the SSLE solver is very obvious, while the posterior value of the MCMC-based solver tends to converge as NSamples increases.

**Fig. 1 Bayesian inference results based on the benchmark case of simply supported beam **
111

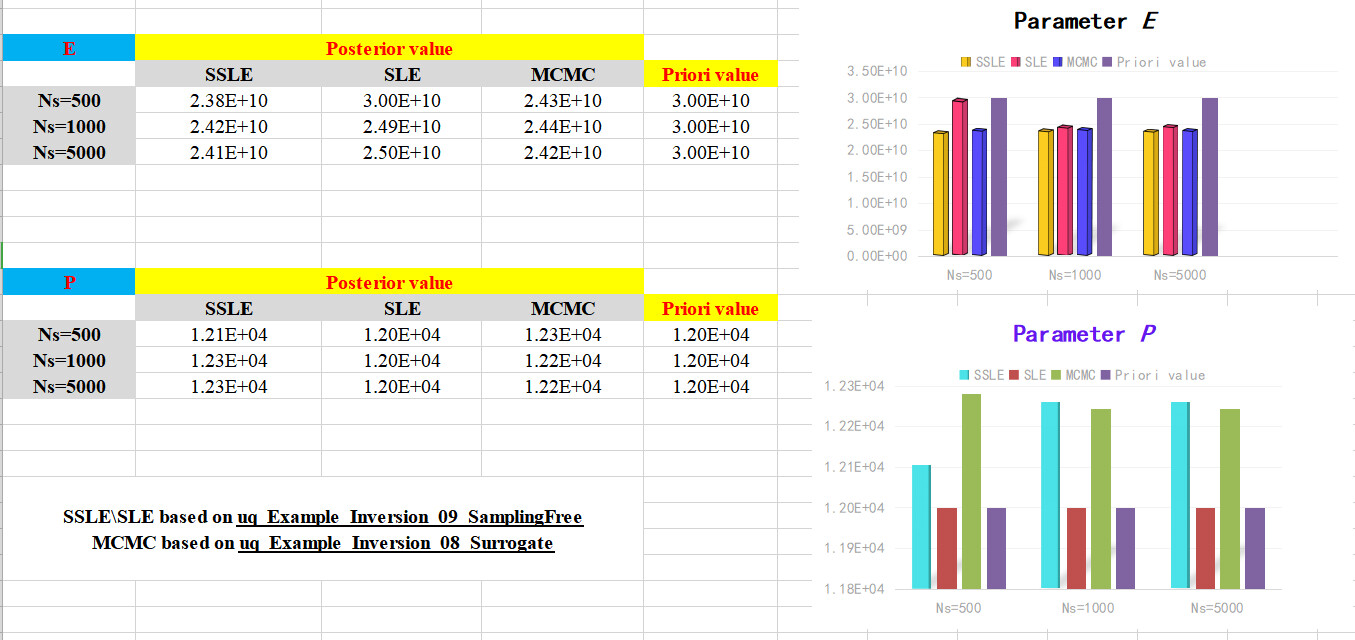
Fig. 2 Bayesian inference results based on external data set
222

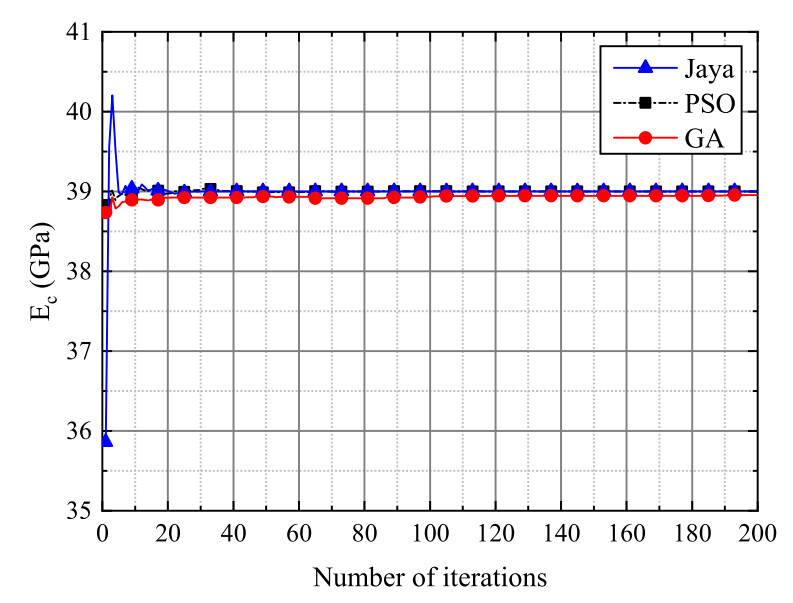
This phenomenon also occurs in a paper I recently submitted, namely, the surrogate-assisted accelerate Bayesian inference, where the parameter posterior value has difficulty converging (but it will converge based on other optimization algorithms), see the following figure：

Fig. 3 Accuracy of Bayesian inversion algorithm based on different surrogate model (in my paper)
333

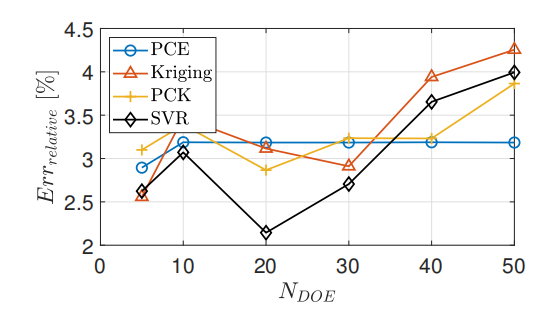
Fig. 4 Parameter identification processes based on Kriging-assisted Jaya algorithm
444

So, I have a few questions

  • What is the reason for this? Is it due to the stochastic nature of Bayesian algorithm or MCMC or SSLE itself?

  • If the posterior value of Bayesian inversion is difficult to converge to a fixed value, then how to judge the inversion accuracy of the algorithm？

  • Is it difficult to achieve the desired results with free sampling applied to black box models?？

1 Like