Explicit expression of the PCE surrogate

UQ with UQLab Community Q&A and How To
,
1

Hi Everyone,

Currently, I am trying to use PCE as a metamodelling (surrogate) model.
I have followed the steps suggested by @bsudret in PCE as a surrogate model for optimization solver.

After getting a metamodel as an uq_model, I can retrieve the coefficients of the PCE surrogate model.

I am looking for an explicit expression of the PCE surrogate so I followed @nluethen 's suggestion in Construct a PCE surrogate using a set of user defined experimental data. I used the MATLAB function polyval to evaluate the function with the coefficients I get from the myPCE.PCE.Coefficients.

However, I failed to do so, and I think it is because UQLab automatically transforms the input (uniform distribution in this case) into standard uniform space. If this is correct, is there any function to transform it back to normal space? I tried the function uq_invNatafTransform, but the third input would cause an error since I only have one marginal (detail below).

E.g. For a polynomial function as the following,

y = -0.5X^3 + 12X^2 + 60X + 0

I am hoping to get a similar result like the figure below for interval X = [0 25], which is also the uniform input distribution.

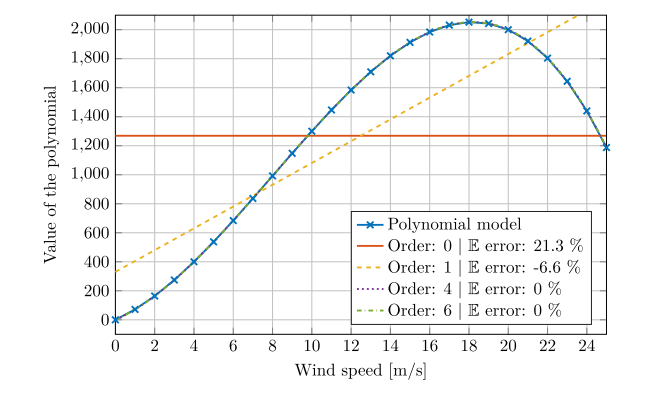
surrogate
(retrieved from Bailleul, W. (2018). Using polynomial chaos expansion for wind energy.)

Instead, I am getting like the following figure using OLS as the method to calculate the coefficients.
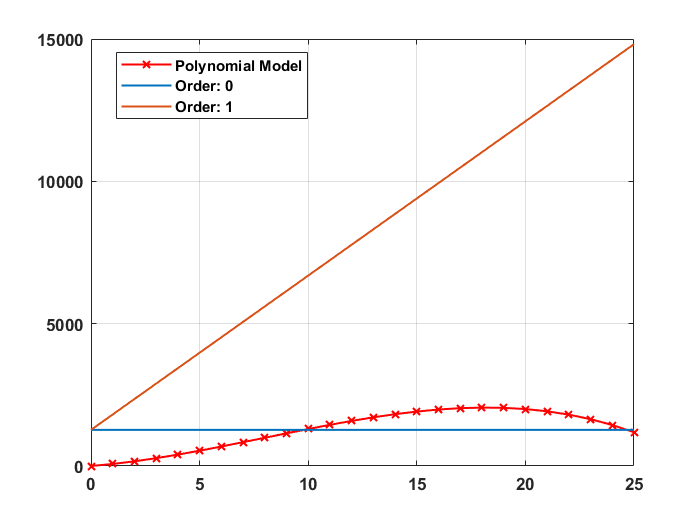
surrogate_failed

I will appreciate any help!

Best regards,
Jason

2

Hi @WindEng,

Thank you for asking here.

  1. If you want to evaluate a PCE model, please use uq_evalModel (see the model manual for more details).

  2. The standard space for uniform distributed variables is [-1,1]. More precisely, a PCE model for X\sim\mathcal{U}(a,b) is evaluated by

    \mathcal{M}^{\rm PCE}(x) = \sum_{i} c_i \Psi_i\left( \frac{2x - b - a}{b-a}\right).

    where \frac{2x - b - a}{b-a} is an affine transformation that maps x\in[a,b] to [-1,1], \Psi_i's are standard Legendre polynomials defined on [-1,1], and c_i's are the associated coefficients.

  3. The built-in function polyval of Matlab uses monomials (i.e. 1,x,x^2,x^3,\ldots) as a basis, which are not orthogonal polynomials (please refer to the the input manual for a more detailed presentation of orthogonal polynomials). Consequently, if you want to keep using polyval, it is important to represent orthogonal polynomials by monomials.

3 Likes