In Owen et al. (2017), the Exp-Tanh function is used to test metamodeling approaches, namely polynomial chaos expansions and Gaussian process modeling.
Description
The Exp-Tanh function is defined as:
where \mathbf{x} = \{x_1, x_2\} are the input variables.
Figure 1 and 2 show the surface and contour plots of the Exp-Tanh function, respectively.
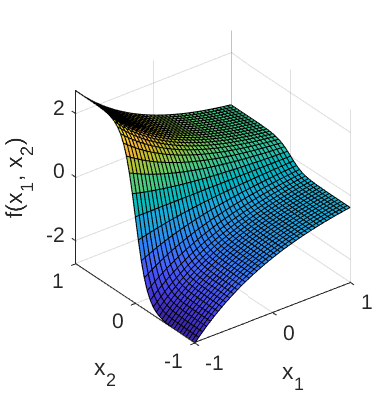
Figure 1: Surface plot of the Exp-Tanh function.
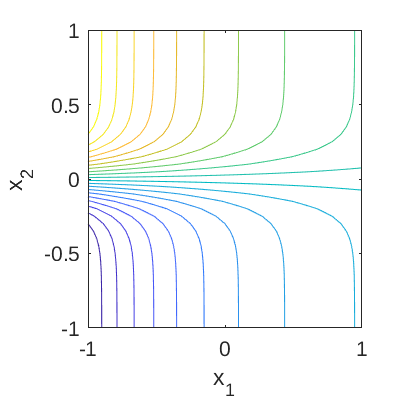
Figure 2: Contour plot of the Exp-Tanh function.
Inputs
For computer experiment purposes, the inputs x_1, x_2 are modeled as two independent uniform random variables.
| No | Variable | Distribution | Parameters |
|---|---|---|---|
| 1 | x_1 | Uniform | x_{1,\min} = -1, x_{1,\max} = 1 |
| 2 | x_2 | Uniform | x_{2,\min} = -1, x_{2,\max} = 1 |
Resources
The vectorized implementation of the Exp-Tanh function in MATLAB as well as the script file with the model and probabilistic inputs definitions for the function in UQLAB can be downloaded below:
uq_expTanh.zip (2.1 KB)
The contents of the file are:
| Filename | Description |
|---|---|
uq_expTanh.m |
vectorized implementation of the Exp-Tanh function |
uq_Example_expTanh.m |
definitions for the model and probabilistic inputs in UQLab |
LICENSE |
license for the function (BSD 3-Clause) |
References
- N. E. Owen, P. Challenor, P. P. Menon, and S. Bennani, “Comparison of surrogate-based uncertainty quantification methods for computationally expensive simulators,” SIAM/ASA Journal on Uncertainty Quantification, vol. 5, no. 1, pp. 403–435, 2017. DOI:10.1137/15M1046812