Hi, everyone,
Many thanks to UQlab for providing customize log-likelihood (log\mathcal{L}) functions and the examples provided are also very helpful.
The working principle for the log\mathcal{L} functions looks simple:
log \mathcal{L} (\boldsymbol{\vec\theta},\boldsymbol{\epsilon} \mid \boldsymbol{Y}) = \left(-\frac{1}{2}\left(\boldsymbol{Y_i} - \mathcal{M}(\vec\theta)\right)^{\mathsf{T}} \boldsymbol{\Sigma}(\epsilon)^{-1}\left(\boldsymbol{Y_i} - \mathcal{M}(\vec\theta)\right)\right) - \frac{3N}{2}\log(2\pi) - \frac{N}{2}\log\left(\det(\boldsymbol{\Sigma}(\epsilon))\right)
During the random walking, current step log\mathcal{L} value choose to stay or to step to next sampling point for MCMC. So, from my understanding, the absolute value for log\mathcal{L} doesnot affect MCMC results. Because it is just doing comparisons. So, I will expect such results that if i do the multiplication log\mathcal{L} \times 5 or log\mathcal{L} \times 500, the MCMC results should not change.
But when i tried, the MCMC result is greatly affected by the absolute value of log\mathcal{L}. The bigger number I mutiply, the corner plotting shrink more. And i dont why.
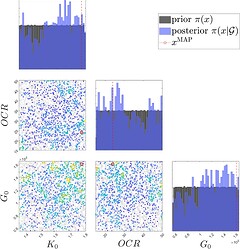
- Case 1: log\mathcal{L} * 5
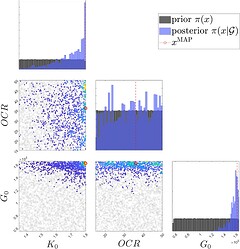
- Case 2: log\mathcal{L}*500
I think it is my misunderstanding for MCMC process rather than the code itself. Any help and advice is appreciated.
Best,
Ningxin
Code is attached.
function logL = uq_inversion_test_func_CustomLogLikelihood(params,data,A)
% UQ_INVERSION_TEST_FUNC_CUSTOMLOGLIKELIHOOD supplies a custom
% logLikelihood handle for the Bayesian inversion module self tests.
%
% See also: UQ_SELFTEST_UQ_INVERSION
%split params into model and error params
modelParams = params(:,1:8);
errorParams = params(:,9:end);
%initialize
sigma = errorParams(:,1); %error standard deviation
psi = errorParams(:,2); %correlation length
nData = size(data,2);
%number of parameters passed to likelihood function
nChains = size(modelParams,1);
%evaluate model
modelRuns = modelParams*A;
%correlation options
CorrOptions.Type = 'Ellipsoidal';
CorrOptions.Family = 'Matern-5_2';
CorrOptions.Isotropic = false;
CorrOptions.Nugget = 0;
%loop through chains
logL = zeros(nChains,1);
for ii = 1:nChains
%get the sigma matrix
sigmaCurr = sigma(ii)*ones(1,nData);
D = diag(sigmaCurr);
%get correlation & covariance matrix
R = uq_eval_Kernel((1:nData).',(1:nData).', psi(ii), CorrOptions);
logLikeli = 0;
C = D*R*D;
L = chol(C,'lower');
Linv = inv(L);
%compute inverse of covariance matrix and log determinante
Cinv = Linv.'*Linv;
logCdet = 2*trace(log(L));
% evaluate log likelihood
logLikeli = logLikeli - 1/2*logCdet - 1/2*diag((data...
-modelRuns(ii,:))*Cinv*(data-modelRuns(ii,:)).');
%assign to logL vector
logL(ii) = logLikeli;
%logL(ii) = logLikeli .* 500; % or i multiply 500 times bigger
end