Connect uqlab with stiffness-method (Statics with matrices) - Question/ Problems with matrices

UQ with UQLab Community Q&A and How To
1

Hello Dear UQ-Team / UQ -user

I am a structural engineer (in my Masters) an have the following question/problem:

I programmed a Matlab-Algorithm to solve static systems (undetermined) with the Stiffness-Method (“Deformationsmethode”). So I have an algorithm which is solved by linear algebra.

Now I thought, that it would be nice to implement some uncertainties (Forces and Young Modulus for instance) and connect it with UQLab (For Multi Storey Frames, etc.),

So my Limit State Function is actually a limited deformation at the top of the building.

The Problem now is the array of the matrices. So when I want to do FORM, Monte Carlo or AK-MCS, of course the dimensions of the matrix does not agree. In a first step I would like to do a FORM an SORM analysis and then for more complex systems use the PCE.

This Pseudo Code is used:

Function g= lsf(X)

% X is a vector containing all your model parameters. The size should be the same as the myInput object that you will create to define input distributions. 

% pass X to your FE code
Here you should pass the values in X to the various arrays/ matrices you need for your FE analysis, ie forces in F, Young’s moduli in the local stiffness matrices etc. 

% run you FE analysis with current values of X
Here you solve for the displacement vector U= K\F

% retrieve the relevant displacement 
utop = U( put here the right index depending on your node/ DOF numbering );

% compute g
g= your_threshold - utop;

The main question is how to pass the vector X to my FE Code ( with X(:,1) it doesn’t work because of the dimensions of the matrices). How do I have to pass these values to my code?

Here is a part of my code or better, of my Limit State function:

function Y = DefMet_USP(X)

%%Lösungsalgorithmus Deformationsmethode

%% E-Moduli und Kräfte

Aa = 0.003; % m^2
Ja = 2*10^-4; %m^4
Jb = 2*10^-4;
Ab = 0.003;
Ac = 0.003;
Ad = 0.003;
Ae = 0.003;


P2 = X(1); --> Here is the problem

E = X(2);   --> Here is the problem


EAa = 100000000000;
EJa = E*Ja;
EJb = E*Jb;
EAb = 100000000000;
EAc = E*Ac;
EAd = E*Ad;
EAe = E*Ae;



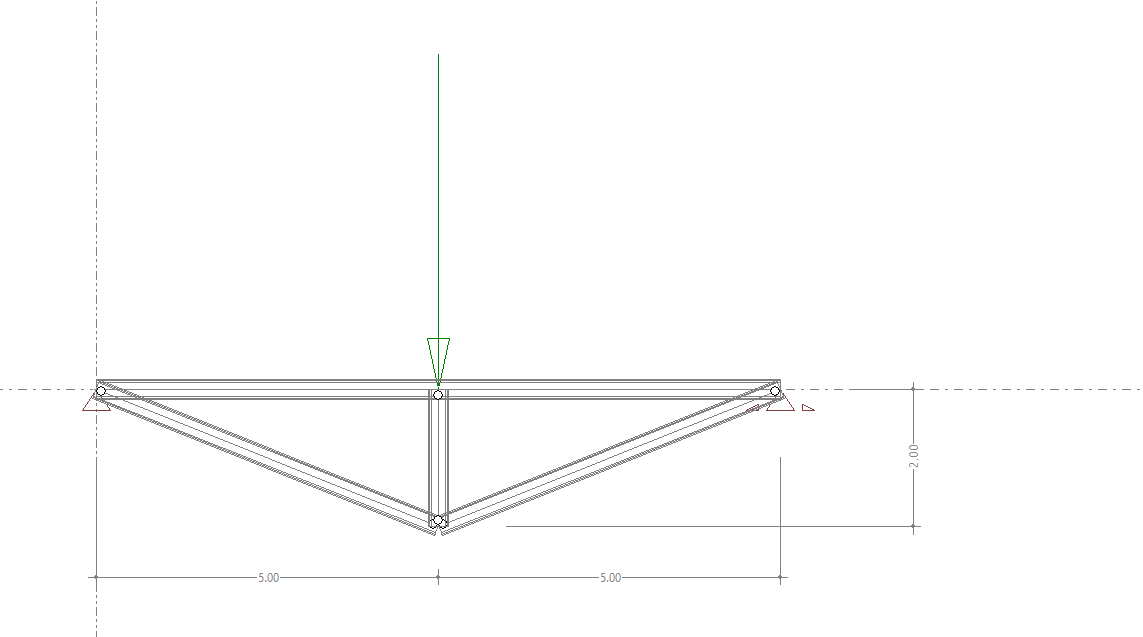
%% Geometrie definieren [m]
La = 5;
Lb = 5;
Lc = sqrt(5^2+2^2);
Ld = 2;
Le = sqrt(5^2+2^2);

%% Lösungsalgorithmus

%Kinematische Matrix definieren

Af=[1 0 0 0 0 0; 
0 -1/Lb 1 0 0 0; 
-1 0 0 1 0 0; 
0 1/Lb 1 0 0 0; 
0 0 0 0 -Ld/(sqrt(5^2+2^2)) La/(sqrt(5^2+2^2)); 
0 1 0 0 -1 0; 
0 0 0 La/(sqrt(5^2+2^2)) -Ld/(sqrt(5^2+2^2)) -La/(sqrt(5^2+2^2))];

%Stabsteifigkeitsmatrix erstellen

K=zeros(7,7);
K(1,1)= EAa/La;
K(2,2)= 3*EJa/La;
K(3,3)= EAb/Lb;
K(4,4)= 3*EJb/Lb;
K(5,5)= EAc/Lc;
K(6,6)= EAd/Ld;
K(7,7)= EAe/Le;


%Knotenlasten

Pf = [0 -P2 0 0 0 0]';
Pwf = [0 0 0 0 0 0]';

%Stabeinspannmomente Q definieren

Q0 = [0; 0; 0; 0; 0; 0; 0;];

%Globale Steifigkeitsmatrix
Ks = Af'*K*Af;


%Lösen Gleichungssystem


Knotenverschiebungen

Uf = Ks^(-1)*(Pf-Pwf-Af'*Q0);

%Berechnung Stabverformungen

V=Af*Uf;


%Berechnung Stabkräfte

Q=K*V+Q0;

%% Limit State Function (Durchbiegungsbegrenzung)

Y = (La+Lb)/300+Uf(2);
end

Thank you really much for your answers, it would be really cool if I had a solution to this problem, before I start using UQ Link with other FE-Programs.

Best regards

Timon

2

Dear Timon,

Your code is difficult to read. You can properly format the code in your post by enclosing it in three apostrophes, for example:

% Knotemverschiebungen
Uf = Ks^(-1)*(Pf-Pwf-Af’*Q0);

As for your problem, I’m not sure I understand you correctly. You have a matrix X containing your inputs (according to your code snippets, each column is an input vector containing all the parameters for a single model evaluation) for the reliability analysis, but there is a mismatch in the dimensions when you pass it to your FEM code? It looks like you are messing up the shape of X. What is the shape of X (or X(:,i) which your actually passing to the FEM code) and what shape should the input to your FEM code be?

Best regards,
Styfen

3

Dear Styen

First, Thank you for your answer. I already saw it that looks strange.

To the problem. The code itself is not the problem, I work with this for many years to solve static undeterminded systems. My problem is to pass the uncertain variables of a vector X to this code.

When we have only a function as limit state function, it would be easy with the Input variables:

P = X(:,1)
E = X(:,2)

Here I have the mismatch because I work with different matrices. In another M-File, I defined the Input Variables (Here P and E with mean and standard deviation,…) and all the differnet analysis (FORM, SORM, MCS). The Input should only be these two random variables.

I hope you know what I mean… :wink:

Best regards

4

Dear Timon,

I’m still not entirely clear about your problem. The problem you are trying to solve sounds pretty standard, so you might find help in the UQLink manual:

If that doesn’t help, you can share your full code (your files).

Best regards,
Styfen

6

Dear Styfen
I thank you really much for helping me. The problem was actaually a normal standard “problem”. When one uses Matrices (like in my Matlab-based FE-Code, which is an .m-file) we do not need to use UQ Link. To become plausible results and no problem with matrices, we just have to define our model as follows:

MOpts.mFile = ‘DefMet_USP’;
MOpts.isVectorized = false;
myModel = uq_createModel(MOpts);

So the model is not vectorized, that we can do MCS, FORM and other kind of reliability analysis, but first we have to define the Input-Variables. In this case:

P2 = X(1);
E = X(2);

It is really cool to connect the stiffnes method with UQLab and I think in the future this will become more and more importance.

I am really looking forward to do reliability analysis with complexer systems and effects with uncertain background like wind r earthquake.

A big Thank you goes to the chair of Risk and Safety of ETH Zurich, and as well to Styfen for helping me,

See you soon and best regards

Timon

PS: For those who are interested, I posted the static system as an annex.
Unterspannter_Träger

1 Like