Hello all! I have been working on this project for some time now and it keeps going deeper into UQ - deep enough to create a case study post here to discuss ideas and provide a reference for other engineers who may want to do reliability analyses of complex structures that are collapsing.
Let’s get straight into the hot topic: I have, as expected, finite element structural models of a tall timber buildings for which I would like to carry out risk analyses. Therefore I am interested in the probability of collapse as well as the consequences of that collapse.
Importance intricacies of the models:
- Very heavy (hours to solve)
- Very highly dimensional (thousands of uncertainty inputs)
- Non-smooth outputs (deflections are smooth until a local/global collapse causes them to jump)
- Many failure domains (there are many different ways the buildings can collapse)
- Probability of collapse can be very small (down to 10^-6)
Sounds like hell, right?
A summary of what I am trying to do is: I analyse a building at a given damage scenario (say, a column is removed) and observe the results:

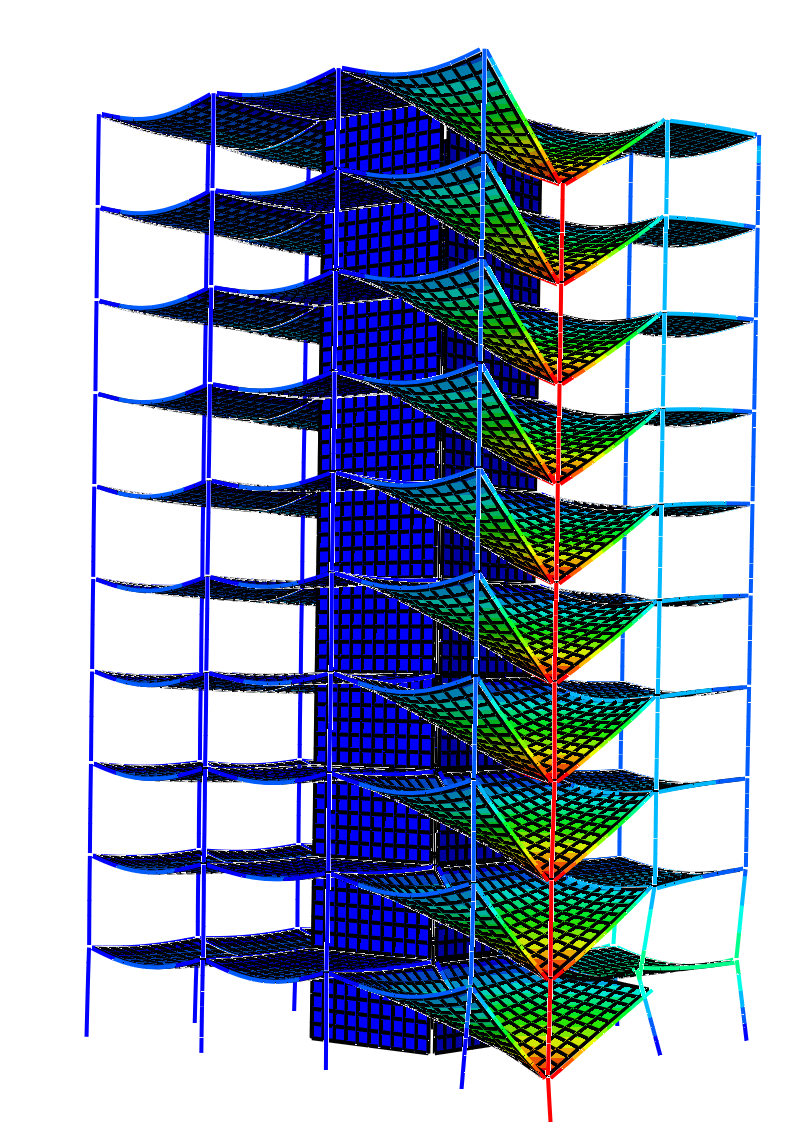
By looking at the final deformations of the floor plates, one can decide if a collapse has occurred or not. To demonstrate this analysis in a simple way, I will use a small 2D frame. See this first example below of this 2D frame which is able to survive with a missing column at the corner.

A 2D matrix representing the structure is constructed, with each element of the matrix corresponding to a bay in the structure. The matrix is populated with the vertical deformations of the centre points of the floor above each bay. If this deformation exceeds a given value, say 1m, a failure flag is raised. Therefore, a matrix of ones and zeros represents the collapse class of the structure. In addition, if we sum the floor areas of all the collapsing bays, we can quantify the extent of the collapse in square meters.
Now consider the same 2D frame, but in this particular realisation of the input vector the entire left section has collapsed. The deformations matrix, failure flags, collapse class, and failure area are calculated:

In a similar manner, different realisations may lead to different collapse classes:


In theory there can be very many collapse classes, but in any given damage scenario only a few of them will probably occur. Note that if the building is well designed, the probability of these collapse classes occurring can be lower than 10^-6. If, on the other hand, we are analysing a poorly designed building, the probability of one collapse classes occurring may be near 1, with some other collapse classes having a probability around 10^-1 or 10^-2.
The tough question: can an adaptive metamodelling algorithm be built to use the least possible amount of data and be able to predict the most probable collapse classes given a new input vector realisation? I am aware of combinations of Kriging with Monte Carlo and Importance Sampling, but at this stage this is an open question.
Second tough question: how can I reduce the dimensionality of this model? Clearly, with thousands of dimensions I am asking for trouble.
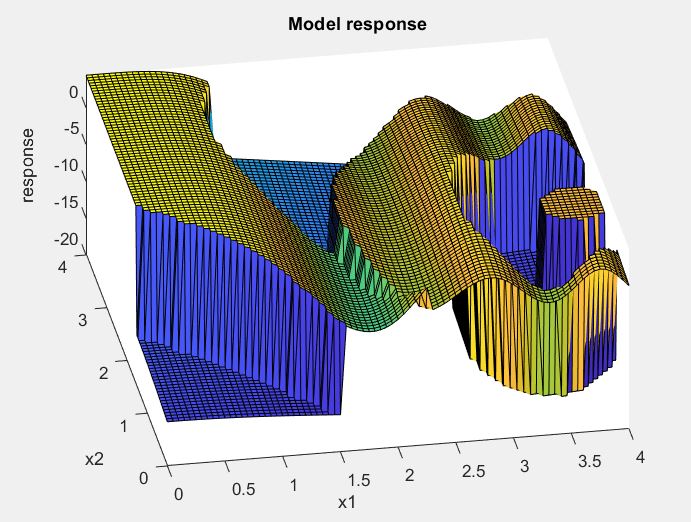
To give a more generic example of the type of model I am trying to surrogate, here is a silly analytical equation I built with some conditional statements to make its response non-smooth (extreme “jumps” just like I expect the deformations of my building to be) and with multiple disjointed domains differing response (just like the existence of different collapse classes). I hope it makes sense/is a good representation.
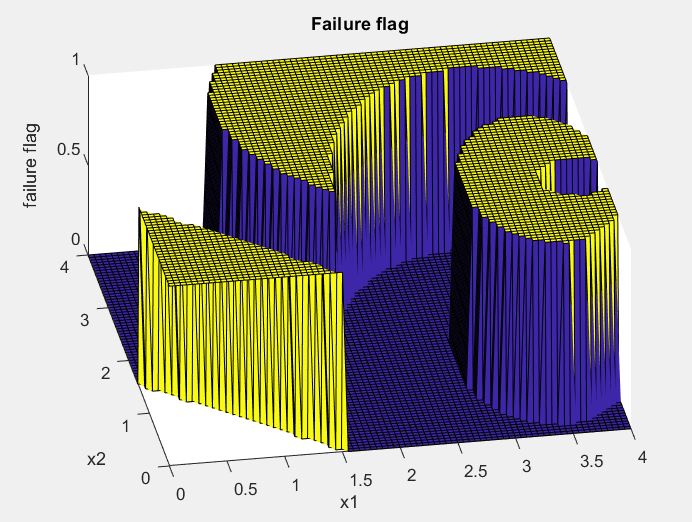
Here is the same plot but with an overall collapse flag of zero or one (pretty much a limit state “function”):
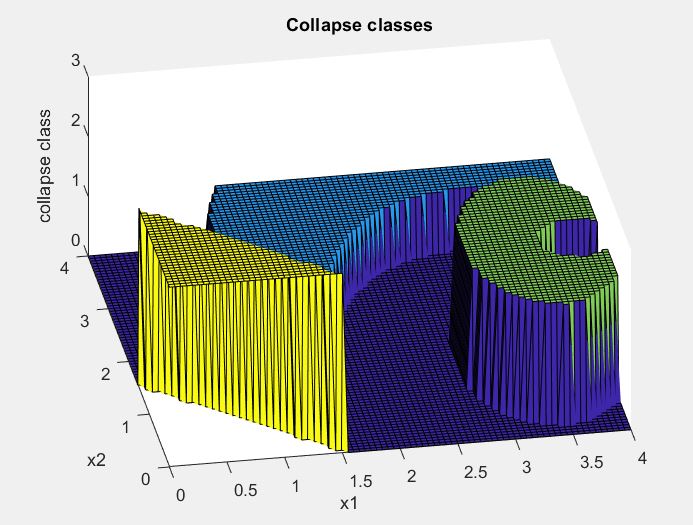
…however I am not interested in just a zero or a one: rather, each time I have a collapse I calculate the area and assign a collapse class. Therefore the plot would look like this:
If you have feedback or ideas to share, please do so here! I will post progress updates when I have them.
Thanks!