Hello,
After several months of intensive use of UQLab and several probabilistic studies on geotechnical cases, I would like to ask a question that has been bothering me for a long time. This question concerns the distributions of experimental design for the creation of meta-models.
Consider a model with two variables:
- phi: friction angle of a soil (Lognormal distribution)
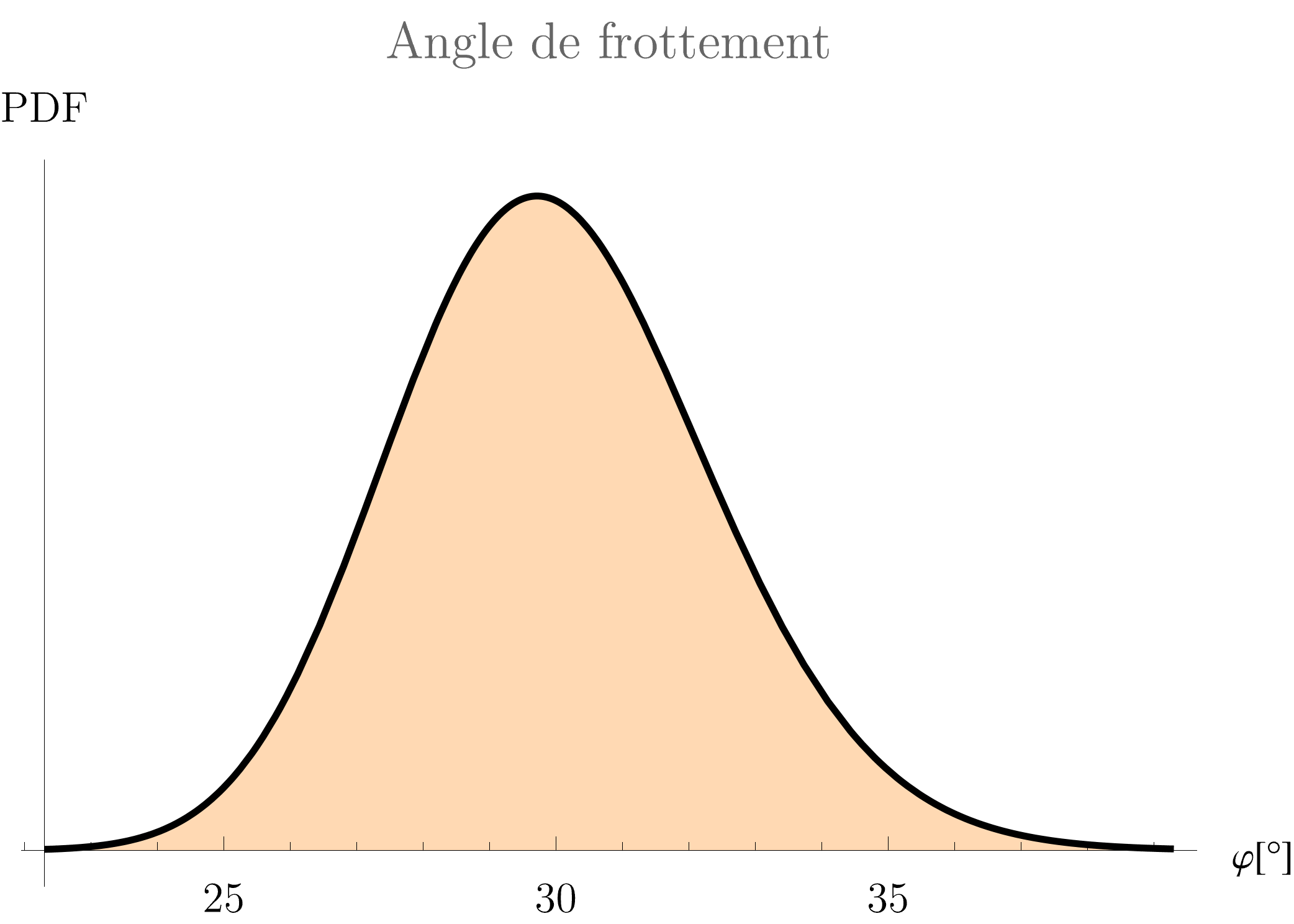
- F: a vertical load (Gumbel distribution)
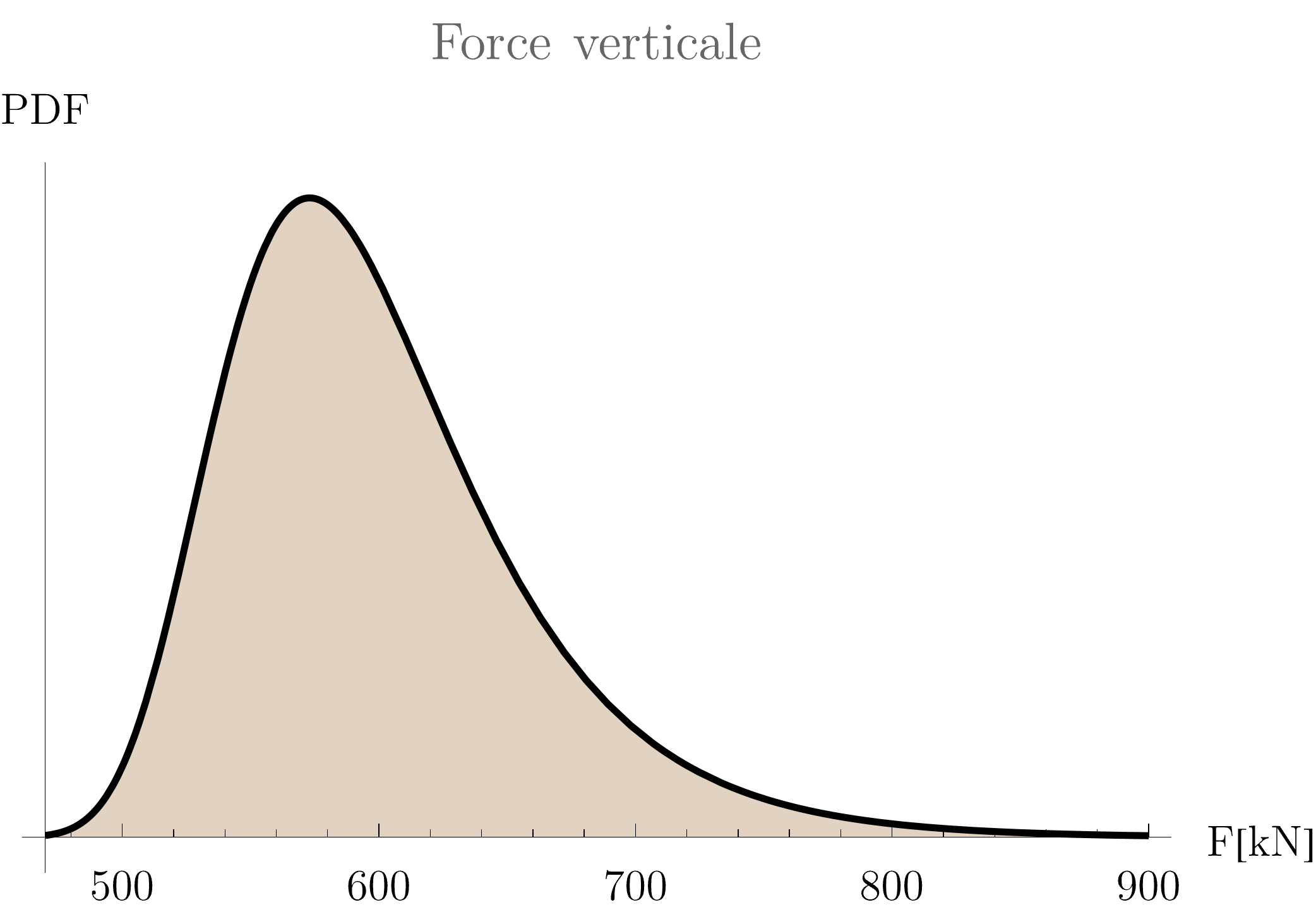
Currently, the experimental design generated by the successive evaluation of a numerical FE model taking as input the “real” above soil distributions. By doing this, one favours the generation of points in the vicinity of the mean values of the distributions, which makes no sense to me given that the quality of the meta-model should be “harmonised” over the domain we are interested in.
Shouldn’t we define a uniform distribution space or even a a regularly spaced grid for the construction of the meta-model and then evaluate it on the true distributions of the problem?
I made an animation comparing the quality convergence of the meta-model as a function of the number of points in the experimental design for a uniform and mixed space. The “true model” in blue represents a PCE containing 1000 sample points (one can surely consider a high precision hence the name “true model”). While it is obviously not possible to make any conclusions from this only one observation, I think it is possible to note the better quality of the meta-model and particularly in the edges (where a reliability analysis would be performed).
I would welcome expert advice.
Video : https://youtu.be/9tyIVxp_oVI