Hi, @damarginal, @bsudret, @nluethen 
the last question is, I want to use the PCE module to calculate skewness and kurtosis of limit state function.
In uq_PCE_calculate_coefficients.m file, I added calculation commands for skewness and kurtosis, but it seems wrong, can you check it for me? Ske~Skewness；Kur~Kurtosis
The code as following:
current_model.PCE(oo).Moments.Mean = current_model.PCE(oo).Coefficients(1);
current_model.PCE(oo).Moments.Var = sum(current_model.PCE(oo).Coefficients(2:end).^2);
current_model.PCE(oo).Moments.Ske =
sum(current_model.PCE(oo).Coefficients(3:end).^3)./sum(current_model.PCE(oo).Coefficients(2:end).^3);
current_model.PCE(oo).Moments.Kur = sum(current_model.PCE(oo).Coefficients(4:end).^4)./sum(current_model.PCE(oo).Coefficients(2:end).^4);
Thank you very much!
Best wishes,
QZ
Hi @Qiang_Zhang,
It’s a good idea to focus your question in the forum to one main problem. If you have another question about a different problem, just open a new topic 
!
It would also be nice to take the time to format your question a bit. If you want to put code, write it using a code block in the editor. If you are referring to a particular part in source code, perhaps mention the line number as well. You might also want to use math to express a formula or an equation. This would make things a bit easier for the people in UQWorld to read your question and, hopefully, help you faster. Thanks !
Hi @Qiang_Zhang, now to your question:
Are you sure these formulas to compute skewness and kurtosis from PCE coefficients are correct? Where did you find them, can you provide a reference? According to Sudret (2017): Polynomial chaos expansions and stochastic finite element methods (section 4.1), skewness and kurtosis have analytical expressions only for Hermite PCE. You can compute them of course numerically by quadrature or MC.
Dear @Qiang_Zhang
As mentioned by Nora, your equations are not correct to compute skewness and kurtosis coefficients.
The 3rd (resp 4-th) order moments requires computing the expectation of products of 3 (resp. 4) polynomials. For Hermite polynomials analytical expressions exist, see eg the appendix of this paper.
Otherwise (e.g. for generalized PCE), you should either use a huge Monte Carlo simulation or quadrature methods.
Best regards
@bsudret @nluethen Thank you very much. I want to calculate the 3rd (4-th) order moments for Hermite PCE. In your papers, the expression of skewness and kurtosis as follows:
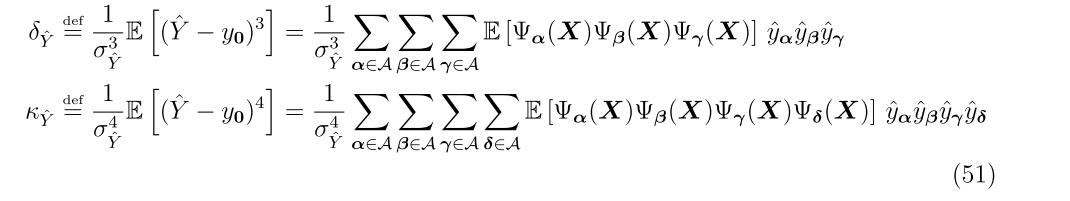
In addition, this is my Matlab code (uq_PCE_calculate_coefficients.m):
current_model.PCE(oo).Moments.Ske = sum(current_model.PCE(oo).Coefficients(1).*current_model.PCE(oo).Coefficients(2).*current_model.PCE(oo).Coefficients(3))./sum(current_model.PCE(oo).Coefficients(2:end).^3);
current_model.PCE(oo).Moments.Kur = sum(current_model.PCE(oo).Coefficients(1).*current_model.PCE(oo).Coefficients(2).*current_model.PCE(oo).Coefficients(3).*current_model.PCE(oo).Coefficients(4))…
./sum(current_model.PCE(oo).Coefficients(2:end).^4);
As above, by comparison with MCS, it still does not match well. Can you help me to check this Matlab code? Thank you very much!
Best regards,
QZ
Hi @Qiang_Zhang,
Your Matlab code does not implement the formulas that you are citing. To compute the expectations, you need to compute the expectations of all possible products of three basis polynomials, and multiply them with the corresponding coefficients, and then sum the terms up. If you are using Hermite polynomials, the expectations on the right-hand side can be computed analytically, as Bruno said:
Also, the factors \frac{1}{\sigma_{\hat Y}^3} and \frac{1}{\sigma_{\hat Y}^4} are not computed correctly in your code. Think about how the standard deviation is computed, and take the correct power of this expression.
It is a bit tricky to get all the expressions right, be patient and implement it step-by-step! Good luck! 