The Branin function is commonly used as a test function for metamodeling in computer experiments, especially in the context of optimization (Forrester et al., 2008; Picheny et al., 2012).
Description
The analytic expression of the Branin function is given as:
where \mathbf{x} = \{x_1, x_2\} are input variables; and a, b, c, r, s, t are constants.
Figure 1 and 2 show the surface and contour plots of the Branin function using the default values of the constants, respectively.
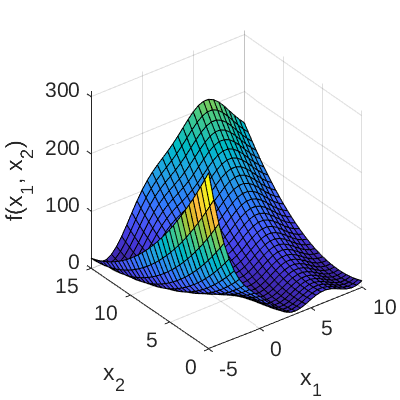
Figure 1: Surface plot of the Branin function.
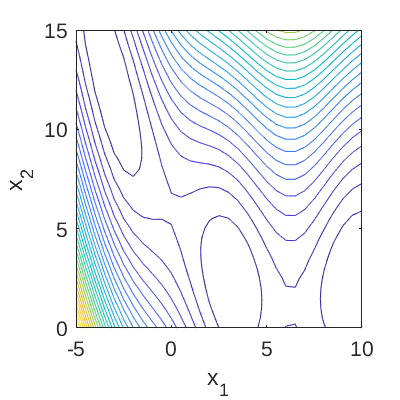
Figure 2: Contour plot of the Branin function.
Inputs
For computer experiments, the input variables x_1, x_2 are modeled as two independent uniform random variables.
| No | Variable | Distribution | Parameters |
|---|---|---|---|
| 1 | x_1 | Uniform |
x_{1,\min} = -5, x_{1,\max} = 10 |
| 2 | x_2 | Uniform |
x_{2,\min} = 0, x_{2,\max} = 15 |
Constants
The default values for the constants are shown below.
| No | Constant | Value |
|---|---|---|
| 1 | a | 1 |
| 2 | b | \frac{5.1}{(2 \pi)^2} |
| 3 | c | \frac{5}{\pi} |
| 4 | r | 6 |
| 5 | s | 10 |
| 6 | t | \frac{1}{8\pi} |
Reference values
Using the constants above, three (identical) global minima of the function, f(\mathbf{x}^*_i) = 0.397887, are located at:
- \mathbf{x}^*_{1} = (-\pi, 12.275)
- \mathbf{x}^*_{2} = (\pi, 2.275)
- \mathbf{x}^*_{3} = (9.42478, 2.475)
Resources
The vectorized implementation of the Branin function in MATLAB as well as the script file with the model and probabilistic inputs definitions for the function in UQLAB can be downloaded below:
uq_branin.zip (2.4 KB)
The contents of the file are:
| Filename | Description |
|---|---|
uq_branin.m |
vectorized implementation of the Branin function |
uq_Example_branin.m |
definitions for the model and probabilistic inputs in UQLab |
LICENSE |
license for the function (BSD 3-Clause) |
References
- A. Forrester, A. Sóbester, and A. Keane, Engineering Design via Surrogate Modelling: A Practical Guide, West Sussex: John Wiley & Sons Ltd., 2008, pp. 196-197. DOI:10.1002/9780470770801
- V. Picheny, T. Wagner, and D. Ginsbourger, “A benchmark of Kriging-based infill criteria for noisy optimization,” HAL, hal-00658212, 2012. URL