Benchmark case - Undamped Oscillator

UQ Resources Benchmarks
1

Undamped (Gayton) Oscillator

The undamped oscillator (Echard et al., 2013) was proposed as a performance function to compare different algorithms for computation of the probability of failure. It is a non-linear, undamped system with a single degree of freedom.

Description

The performance of an undamped oscillator due to an impulse of lenght T_1 is defined as:

f(\mathbf{x}, \omega_0) = 3R - \left| \frac{2F_1}{M \omega_0^2} \sin\left(\frac{\omega_0 T_1}{2}\right) \right|,

where \omega_0 is a natural frequency of the oscillator defined as

\omega_0 = \sqrt{\frac{C_1 + C_2}{M}}

and \mathbf{x} = \{R, C_1, C_2, M, R, F_1, T_1\} are independent Gaussian input variables.

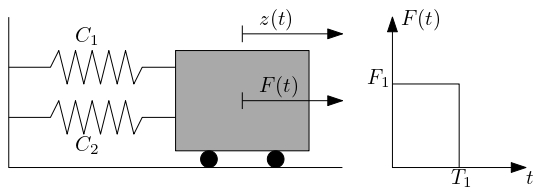
UndampedOscillator
Figure 1: Undamped non-linear oscillator, adapted from Echard et al. (2013)

Inputs

For computer experiment purposes, the inputs R, C_1, C_2, M, R, F_1, T_1 are modeled as six independent Gaussian random variables.

No Variable Description Distribution Statistics
1 C_1 First spring constant Gaussian \mu_{C_1} = 1,
\text{COV}_{C_1} = 10\%
2 C_2 Second spring constant Gaussian \mu_{C_2} = 0.1,
\text{COV}_{C_2} = 10\%
3 M Oscillator mass Gaussian \mu_{M} = 1,
\text{COV}_{M} = 5\%
4 R Yield displacement Gaussian \mu_{R} = 0.5,
\text{COV}_{R} = 10\%
5 F_1 Force acting on oscillator Gaussian \mu_{F_1} = 0.6,
\text{COV}_{F_1} = 16.67\%
6 T_1 Time interval the force is acting on the oscillator Gaussian \mu_{T_1} = 1,
\text{COV}_{T_1} = 20\%

Resources

The vectorized implementation of the undamped oscillator in MATLAB, as well as the script file with the model and probabilistic inputs definitions for the function in UQLab, can be downloaded below:

uq_undampedOscillator.zip (2.6 KB)

The contents of the file are:

Filename Description
uq_undampedOscillator.m vectorized implementation of the undamped oscillator model in MATLAB
uq_Example_undampedOscillator.m definitions for the model and probabilistic inputs in UQLab
LICENSE license for the function (BSD 3-Clause)

Open-access repository

The dataset used in this benchmark study is titled “Benchmark case datasets - Undamped Oscillator” and is authored by Adéla Hlobilová, Stefano Marelli, and Bruno Sudret. It was published in 2024 and is available on Zenodo. The dataset can be accessed directly via the following DOI link: 10.5281/zenodo.12685553.

The experimental designs include datasets with 40, 80, 120, 160, and 200 samples, each generated using optimized Latin Hypercube Sampling (LHS) with 1,000 iterations to improve the maximin criterion. Each dataset is replicated 20 times. The validation set contains 100,000 samples generated by Monte Carlo simulation. Each dataset contains samples and responses of the computational model.

For citation purposes, please use the following format:
Hlobilová, A., Marelli, S., and Sudret, B. (2024). Benchmark case datasets - Undamped Oscillator. Zenodo. https://doi.org/10.5281/zenodo.12685553.

This project was supported by the Open Research Data Program of the ETH Board under Grant number EPFL SCR0902285.

References

  • Echard, B., Gayton, N., Lemaire, M., Relun, N. “A combined Importance Sampling and Kriging reliability method for small failure probabilities with time-demanding numerical models,” Reliability Engineering & System Safety, vol. 111, pp. 232-240, 2013. DOI:10.1016/j.ress.2012.10.008
  • Lüthen, N., Marelli, S., Sudret, B. “Sparse Polynomial Chaos Expansions: Literature Survey and Benchmark,” SIAM/ASA Journal on Uncertainty Quantification, vol. 9, issue 2, pp. 593–649, 2021. DOI:10.1137/20M1315774