Benchmark case - One-dimensional diffusion model

UQ Resources Benchmarks
1

The one-dimensional diffusion model

The one-dimensional diffusion model is a standard benchmark in UQ computations used in Shin and Xiu (2016), Fajraoui et al. (2017), and Lüthen et al. (2021).

Description

This model corresponds to a one-dimensional diffusion equation with a (spatially) uncertain diffusion coefficient. The problem is defined over a domain D = [0, L], governed by the boundary value problem:

- \frac{d}{dx} \left[ E(x, \omega) \frac{du}{dx}(x, \omega) \right] + f(x) = 0,

with boundary conditions:

u(0) = 0, \quad \frac{du}{dx}(L) = F.

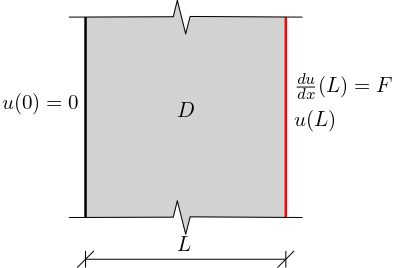
1dimDiffusion
Figure 1: Domain and boundary conditions of the one-dimensional diffusion model.

Here, the diffusion coefficient E(x, \omega) is modeled as a log-normal random field:

E(x, \omega) = \exp(\lambda_E + \zeta_E \,g(x, \omega)),

where g(x, \omega) is a standard normal stationary Gaussian random field with an exponential autocorrelation function:

\rho(x, x') = e^{-|x' - x| / l}.

The Gaussian field g(x, \omega) is approximated using the Karhunen–Loève expansion:

g(x, \omega) = \sum_{k=1}^{M} \sqrt{\lambda_k} \varphi_k(x) \xi_k(\omega),

where \{(\lambda_k, \varphi_k), k = 1, \ldots, M \} are the solutions of the Fredholm equation associated with the exponential kernel.

For numerical experimentation, the parameters are set to the following values:

  • Domain length: L = 1

  • Flux at the right boundary: F = 1

  • Source term of the diffusing quantity: f(x) = 0.5

  • Mean of the log of the diffusion coefficient field: \lambda_E = 10

  • Standard deviation of the log of the diffusion coefficient field: \zeta_E = 3

  • Length scale of the exponential autocorrelation function of the Gaussian random field: l = 1/3

The number of terms M = 62 is chosen such that:

\sum_{k=1}^{M} \lambda_k / \sum_{k=1}^{\infty} \lambda_k \geq 0.99.

The response quantity of interest is the diffusion at the right boundary of the domain, u(L).

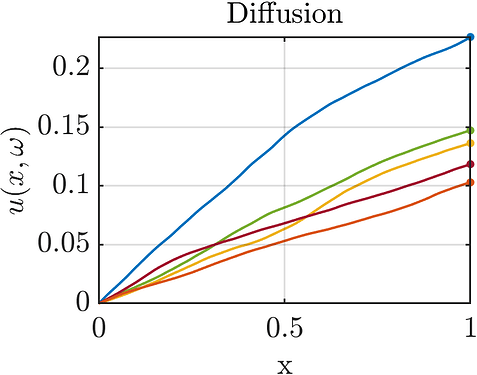
1Ddiffusion_diff
1Ddiffusion_diff801×629 26.9 KB

Figure 2: Diffusion u(x, \omega) over the D domain for 5 realizations of the random field \omega.

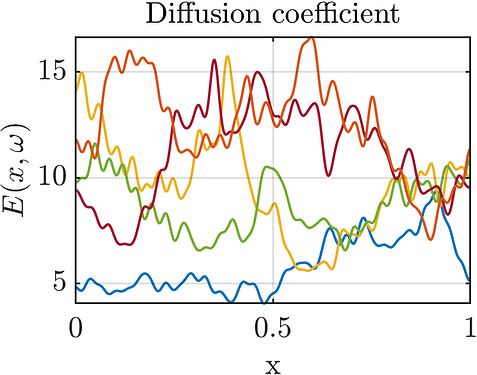
1Ddiffusion_diffCoef
1Ddiffusion_diffCoef801×629 44.9 KB

Figure 3: Diffusion coefficient E(x, \omega) over the D domain for 5 realizations of the random field \omega. The colors for each realization correspond to Figure 2.

Inputs

The one-dimensional diffusion model involves 62 independent Gaussian random variables:

Variable Description Distribution Statistics
X_1 - X_{62} Input variable Gaussian \mu_{X_i} = 0,
\sigma_{X_i} = 1

Open-access repository

The dataset used in this benchmark study is titled “Benchmark case datasets - One-dimensional diffusion model” and is authored by Adéla Hlobilová, Stefano Marelli, and Bruno Sudret. It was published in 2024 and is available on Zenodo. The dataset can be accessed directly via the following DOI link: 10.5281/zenodo.12704504.

The experimental designs include datasets with 200, 400, 600, 800, and 1000 samples, each generated using optimized Latin Hypercube Sampling (LHS) with 1,000 iterations to improve the maximin criterion. Each dataset is replicated 20 times. The validation set contains 100,000 samples generated by Monte Carlo simulation. Each dataset contains samples and responses of the computational model.

For citation purposes, please use the following format:
Hlobilová, A., Marelli, S., and Sudret, B. (2024). Benchmark case datasets - One-dimensional diffusion model. Zenodo. https://doi.org/10.5281/zenodo.12704504.

This project was supported by the Open Research Data Program of the ETH Board under Grant number EPFL SCR0902285.

References

  • Shin, Y., Xiu, D. “Nonadaptive Quasi-Optimal Points Selection for Least Squares Linear Regression,” SIAM Journal on Scientific Computing, vol. 38, issue 1, pp. A385–A411, 2016. DOI:10.1137/15M1015868

  • Fajraoui, N., Marelli, S., Sudret, B. “Sequential Design of Experiment for Sparse Polynomial Chaos Expansions,” SIAM/ASA Journal on Uncertainty Quantification, vol. 5, issue 1, pp. 1061–1085, 2017. DOI:10.1137/16M1103488

  • Lüthen, N., Marelli, S., Sudret, B. “Sparse Polynomial Chaos Expansions: Literature Survey and Benchmark,” SIAM/ASA Journal on Uncertainty Quantification, vol. 9, issue 2, pp. 593–649, 2021. DOI:10.1137/20M1315774