Benchmark case - Morris function

UQ Resources Benchmarks
1

Morris function

The Morris function has been used by Lamboni et al. (2012), Morris (1991) and Blatman and Sudret (2010) to test the performance of sensivity analyses.

Description

The performance function is defined as:

P = \beta_0 + \sum_{i=1}^{20} \beta_i \omega_i + \sum_{i < j}^{20} \beta_{i,j} \omega_i \omega_j + \sum_{i < j < l}^{20} \beta_{i,j,l} \omega_i \omega_j \omega_l + \sum_{i < j < l < s}^{20} \beta_{i,j,l,s} \omega_i \omega_j \omega_l \omega_s

Different definitions of \omega_i and \beta ’s exist, we use the same as in Blatman and Sudret (2010):

  • \omega_i = 2(X_i - \frac{1}{2}) for i \in \{1, 2, \ldots, 20\} and i \notin \{3, 5, 7\}
  • \omega_i = 2\left(1.1 \frac{X_i}{X_i + 0.1} - \frac{1}{2}\right) for i \in \{3, 5, 7\}
  • \beta_i = 20 for i \in \{1, 2, \ldots, 10\}
  • \beta_{i,j} = -15 for i, j \in \{1, 2, \ldots, 6\} and i < j
  • \beta_{i,j,l} = -10 for i, j, l \in \{1, 2, \ldots, 5\} and i < j < l
  • \beta_{1,2,3,4} = 5
  • \beta_i = (-1)^i for i \in \{11, 12, \ldots, 20\}
  • \beta_{i,j} = (-1)^{i+j} for i \in \{1, 2, \ldots, 20\} and j \in \{7, 8, \ldots, 20\} and i < j
  • \beta_{i,j,l} = 0 for i \in \{1, 2, \ldots, 20\}, j \in \{1, 2, \ldots, 20\}, l \in \{6, 7, \ldots, 20\} and i < j < l
  • \beta_{i,j,l,s} = 0 for i \ne 1, j \ne 2, l \ne 3, s \ne 4

where:

  • X_i: Random variables
  • \omega_i: Functions of the random variables
  • \beta: Coefficients

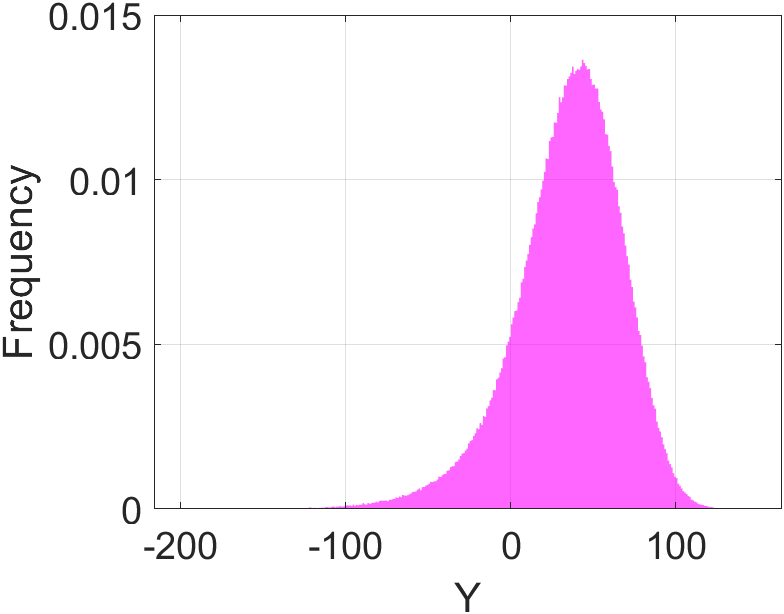
Morris_response_histogram
Morris_response_histogram784×614 8.4 KB

Figure 1: The histogram of the Morris function output when using uniform input distributions (see details below for the version by Blatman and Sudret (2010)) based on 10^6 sample points.

Inputs

The Morris function problem involves twenty independent random variables. Two specifications exist: one employs uniformly distributed random variables, while the other encompasses variables from various distributions. We utilize the specification from Blatman and Sudret (2010). For reference, we also present the alternative specification used in the literature by Lamboni (2012).

Version by Blatman and Sudret (2010):

Variable Description Distribution Parameters
X_1 - X_{20} Input variable Uniform [0, \, 1]

Version by Lamboni (2012):

Variable Description Distribution Parameters
X_1 Input variable Uniform U(0,1)
X_2 Input variable Gaussian N(0.5, \sqrt{0.1})
X_3 Input variable Exponential E(4)
X_4 Input variable Gumbel G(0.2, 0.2)
X_5 Input variable Weibull W(0.5, 2)
X_6 - X_{10} Input variable Uniform U(0,1)
X_{11} Input variable Uniform U(0,1)
X_{12} Input variable Gaussian N(0.5, \sqrt{0.1})
X_{13} Input variable Exponential E(4)
X_{14} Input variable Gumbel G(0.2, 0.2)
X_{15} Input variable Weibull W(0.5, 2)
X_{16} - X_{20} Input variable Uniform U(0,1)

Resources

The vectorized implementation of the Morris function in MATLAB, as well as the script file with the model and probabilistic inputs definitions for the function in UQLab, can be downloaded below:

uq_Morris.zip (2.3 KB)

The contents of the file are:

Filename Description
uq_morris.m vectorized implementation of the Morris function in MATLAB
uq_Example_Morris.m definitions for the model and probabilistic inputs in UQLab
LICENSE license for the function (BSD 3-Clause)

Open-access repository

The dataset used in this benchmark study is titled “Benchmark case datasets - Morris function” and is authored by Adéla Hlobilová, Stefano Marelli, and Bruno Sudret. It was published in 2024 and is available on Zenodo. The dataset can be accessed directly via the following DOI link: 10.5281/zenodo.12700514.

The experimental designs include datasets with 400, 800, 1200, 1600, and 2000 samples, each generated using optimized Latin Hypercube Sampling (LHS) with 1,000 iterations to improve the maximin criterion. Each dataset is replicated 20 times. The validation set contains 100,000 samples generated by Monte Carlo simulation. Each dataset contains samples and responses of the computational model.

For citation purposes, please use the following format:
Hlobilová, A., Marelli, S., and Sudret, B. (2024). Benchmark case datasets - Morris function. Zenodo. https://doi.org/10.5281/zenodo.12700514.

This project was supported by the Open Research Data Program of the ETH Board under Grant number EPFL SCR0902285.

References

  • Blatman, G., B. Sudret. “Efficient computation of global sensitivity indices using sparse polynomial chaos expansions,” Reliability Engineering & System Safety, vol. 95, issue 11, pp. 1216–-1229, 2010. DOI:10.1016/j.ress.2010.06.015
  • Lamboni, M., B. Iooss, A.-L. Popelin, F. Gamboa. “Derivative-based global sensitivity measures: general links with Sobol’ indices and numerical tests,” Mathematics and Computers in Simulation, vol. 87, pp. 45–54, 2012. DOI:10.1016/j.matcom.2013.02.002
  • Morris, M. “Factorial sampling plans for preliminary computational experiments,” Technometrics, vol. 33, no. 2, pp. 161-–174, 1991. DOI:10.2307/1269043
  • Lüthen, N., Marelli, S., Sudret, B. “Sparse Polynomial Chaos Expansions: Literature Survey and Benchmark,” SIAM/ASA Journal on Uncertainty Quantification, vol. 9, issue 2, pp. 593–649, 2021. DOI:10.1137/20M1315774