Damped Oscillator
The Damped Oscillator is an example that is commonly used in structural reliability to demonstrate the robustness of the proposed approach for estimating low failure probabilities and their gradients.
Description
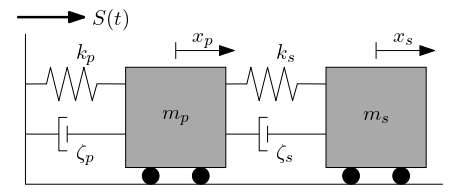
Figure 1 shows the considered two-degree-of-freedom primary-secondary system which is characterized by the masses m_p and m_s, spring stiffnesses k_p and k_s and damping ratios \zeta_p and \zeta_s. The subscripts p and s refer to the primary and secondary oscillators. Finally, the excitation, given by a white noise base acceleration, is represented through S(t).
Figure 1: A two-d.o.f. damped oscillator under a white-noise base acceleration, adapted from Dubourg (2011).
Assuming that the reliability of the entire system can be reduced to the capacity of the secondary spring, one finds a performance function which is defined as follows:
where
- F_s: Force capacity of the secondary spring
- \tau: Duration of the excitation
- x_s: Relative displacement
In the sequel, the maximum is substituted by its mean amplitude since the uncertainty in the peak response is usually small. Hence, the performance function can be rewritten:
where
- p: So-called peak factor, set equal to 3
The mean-square relative displacement of the secondary spring under a white noise base acceleration S can be calculated using the analytic expression shown below:
where
- \omega_p, \omega_s: Natural frequencies, given as
- \omega_p = \sqrt{\frac{k_p}{m_p}}, \omega_s = \sqrt{\frac{k_s}{m_s}}
- S_0: Intensity of the white noise
- \gamma, \omega_a, \zeta_a, \theta: Further abbreviations and ratios, determined through
- \gamma = \frac{m_s}{m_p}
- \omega_a = \frac{\omega_p + \omega_s}{2}
- \zeta_a = \frac{\zeta_p + \zeta_s}{2}
- \theta = \frac{\omega_p - \omega_s}{\omega_a}
Inputs
The Damped Oscillator problem contains eight independent, lognormal distributed random variables X = \{m_p, m_s, k_p, k_s, \zeta_p, \zeta_s, S_0, F_s\}:
| No | Variable | Description | Distribution | Statistics |
|---|---|---|---|---|
| 1 | m_p | Primary mass | Lognormal | \mu_{m_p} = 1.5, \text{CV}_{m_p} = 10\% |
| 2 | m_s | Secondary mass | Lognormal | \mu_{m_s} = 0.01, \text{CV}_{m_s} = 10\% |
| 3 | k_p | Primary spring stiffness | Lognormal | \mu_{k_p} = 1, \text{CV}_{k_p} = 20\% |
| 4 | k_s | Secondary spring stiffness | Lognormal | \mu_{k_s} = 0.01, \text{CV}_{k_s} = 20\% |
| 5 | \zeta_p | Primary damping ratio | Lognormal | \mu_{\zeta_p} = 0.05, \text{CV}_{\zeta_p} = 40\% |
| 6 | \zeta_s | Secondary damping ratio | Lognormal | \mu_{\zeta_s} = 0.02, \text{CV}_{\zeta_s} = 50\% |
| 7 | S_0 | Intensity of the white noise | Lognormal | \mu_{S_0} = 100, \text{CV}_{S_0} = 10\% |
| 8 | F_s | Force capacity of the secondary spring | Lognormal | \mu_{F_s} = \{15, 21.5, 27.5\}, \text{CV}_{F_s} = 10\% |
Constants
The default value of the only constant, the peak factor, is determined as follows:
| Constant | Value |
|---|---|
| p | 3 |
Reference results
The following table lists reference results of the probability of failure P_f for different values of the force capacity of the secondary spring F_s using subset simulation (Dubourg, 2011).
| \mu_{F_s} | 15 | 21.5 | 27.5 |
|---|---|---|---|
| Number of samples N | 300{,}000 | 500{,}000 | 700{,}000 |
| Probability of failure P_f | 4.63 \times 10^{-3} | 4.75 \times 10^{-5} | 3.47 \times 10^{-7} |
| Coefficient of variation CV | <3\% | <4\% | <5\% |
Resources
The vectorized implementation of the damped oscillator in MATLAB, as well as the script file with the model and probabilistic inputs definitions for the function in UQLab, can be downloaded below:
uq_dampedOscillator.zip (2.9 KB)
The contents of the file are:
| Filename | Description |
|---|---|
uq_DampedOscillator.m |
vectorized implementation of the damped oscillator performance function in MATLAB |
uq_Example_dampedOscillator.m |
definitions for the model and probabilistic inputs in UQLab |
LICENSE |
license for the function (BSD 3-Clause) |
Open-access repository
The dataset used in this benchmark study is titled “Benchmark case datasets - Damped oscillator” and is authored by Adéla Hlobilová, Stefano Marelli, and Bruno Sudret. It was published in 2024 and is available on Zenodo. The dataset can be accessed directly via the following DOI link: 10.5281/zenodo.12700167.
The experimental designs include datasets with 400, 800, 1200, 1600, and 2000 samples, each generated using optimized Latin Hypercube Sampling (LHS) with 1,000 iterations to improve the maximin criterion. Each dataset is replicated 20 times. The validation set contains 100,000 samples generated by Monte Carlo simulation. Each dataset contains samples and responses of the computational model.
For citation purposes, please use the following format:
Hlobilová, A., Marelli, S., and Sudret, B. (2024). Benchmark case datasets - Damped oscillator. Zenodo. https://doi.org/10.5281/zenodo.12700167.
This project was supported by the Open Research Data Program of the ETH Board under Grant number EPFL SCR0902285.
References
- Igusa, T., A. Der Kiureghian “Dynamic characterization of two degree-of-freedom equipment-structure systems,” Journal of Engineering Mechanics, vol. 111, issue 1, pp. 1–19, 1985. DOI:10.1061/(ASCE)0733-9399(1985)111:1(1)
- Der Kiureghian, A., De Stefano, M. “An efficient algorithm for second-order reliability analysis,” Technical Report UCB/SEMM-90/20, Department of Civil and Environmental Engineering, University of California, Berkeley, 1990.
- Dubourg, V. Adaptive surrogate models for reliability analysis and reliability-based design optimization. Doctoral thesis, Blaise Pascal University – Clermont II, 2011. PDF file
- Lüthen, N., Marelli, S., Sudret, B. “Sparse Polynomial Chaos Expansions: Literature Survey and Benchmark,” SIAM/ASA Journal on Uncertainty Quantification, vol. 9, issue 2, pp. 593–649, 2021. DOI:10.1137/20M1315774