Hi @yanglechang
So the first problem can be solved right out of the box in the inversion module by setting up the problem as follows:
First, define a simple forward model (identity function)
ModelOpts.mString = 'X';
ModelOpts.isVectorized = true;
myForwardModel = uq_createModel(ModelOpts);
store the measurements
myData.y = [y1; y2; y3; ...; yN];
myData.Name = 'Measurements of y';
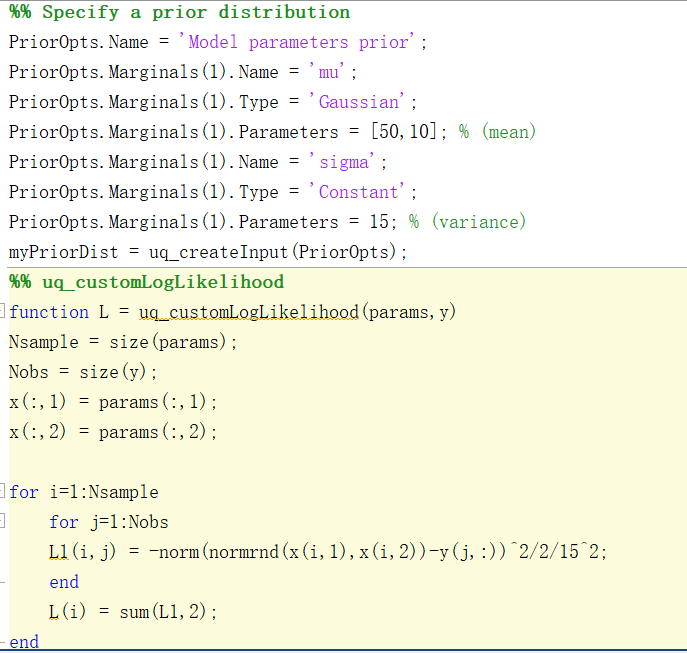
define a prior distribution on \mu
PriorOpts.Marginals.Name = 'mu';
PriorOpts.Marginals.Type = 'Uniform';
PriorOpts.Marginals.Parameters = [a1 b1];
myPriorDist = uq_createInput(PriorOpts);
supply the discrepancy model
SigmaOpts.Marginals.Name = 'Sigma2';
SigmaOpts.Marginals.Type = 'Uniform';
SigmaOpts.Marginals.Parameters = [a2 b2];
mySigmaDist = uq_createInput(SigmaOpts);
DiscrepancyOpts.Type = 'Gaussian';
DiscrepancyOpts.Prior = mySigmaDist;
and finally, define the object that stores all this information
BayesOpts.Type = 'Inversion';
BayesOpts.Data = myData;
BayesOpts.Discrepancy = DiscrepancyOpts;
BayesOpts.Prior = myPriorDist;
That’s it, now you should be able to run the analysis with
myBayesianAnalysis = uq_createAnalysis(BayesOpts);
% Print out a report of the results:
uq_print(myBayesianAnalysis)
% Create a graphical representation of the results:
uq_display(myBayesianAnalysis)
That should do the trick. Keep in mind that this simple hierarchical problem is a very special case that is supported only because it meets the following conditions (I hope I didn’t forget any):
- You assume that X\sim\mathcal{N} (normally distributed) which is incidentally the only provided discrepancy model;
- There are not more than two levels in your problem’s hierarchy;
- You are inferring information about the parameters using observations of those parameters thus reducing the forward model to the identity function \mathcal{M}(\mu)=\mu;
- Implicitly you assume perfect, i.e. noise-free, measurements.
If any of those conditions were not met, you would have to use the user-defined likelihood function feature to set up your problem.
Assume now that you assign a prior \pi(\theta) also on the parameters \mathbf{\theta}=(a_1,a_2,b_1,b_2), the 2. condition in the list above is not met because your problem now has three levels of hierarchy and you would have to extend your Bayesian problem definition to
\pi(\mu\vert\mathcal{X})\propto\pi(\mathcal{X}\vert\mu)\pi(\mu\vert\theta)\pi(\theta).
To fit into the framework provided by the Bayesian module in UQLab, your user-defined likelihood function should then return something like
\mathcal{L}(\theta) = \int \pi(\mathcal{X}\vert\mu)\pi(\mu\vert\theta)\,\mathrm{d}\mu,
i.e. marginalize over the hyper parameter \mu to be a function of only the (hyper-)hyperparameters \theta.
I hope this helps!
, the likelihood is given in the normal distribution form as 
. The prior distribution of the input variable X is also a normal distribution X ~ N( μ , σ ), where the unknown parameters μ and σ fall with the intervals [
] and [
] ( 
are fixed values) repectively. That is μ ~ Uniform (
) , σ ~ Uniform (